Abstract
We obtained New Horizons LORRI images to measure the cosmic optical background (COB) intensity integrated over 0.4 μm ≲ λ ≲ 0.9 μm. The survey comprises 16 high-Galactic-latitude fields selected to minimize scattered diffuse Galactic light (DGL) from the Milky Way, as well as scattered light from bright stars. This work supersedes an earlier analysis based on observations of one of the present fields. Isolating the COB contribution to the raw total sky levels measured in the fields requires subtracting the remaining scattered light from bright stars and galaxies, intensity from faint stars within the fields fainter than the photometric detection limit, and the DGL foreground. DGL is estimated from 350 μm and 550 μm intensities measured by the Planck High Frequency Instrument, using a new self-calibrated indicator based on the 16 fields augmented with eight additional DGL calibration fields obtained as part of the survey. The survey yields a highly significant detection (6.8σ) of the COB at 11.16 ± 1.65 (1.47 sys, 0.75 ran) nW m−2 sr−1 at the LORRI pivot wavelength of 0.608 μm. The estimated integrated intensity from background galaxies, 8.17 ± 1.18 nW m−2 sr−1, can account for the great majority of this signal. The rest of the COB signal, 2.99 ± 2.03 (1.75 sys, 1.03 ran) nW m−2 sr−1, is formally classified as anomalous intensity but is not significantly different from zero. The simplest interpretation is that the COB is completely due to galaxies.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Light from a Dark Universe
At the dawn of time, the Universe was a sea of light. But as it expanded, it cooled, dimmed, and matter came to the fore. Nearly 14 billion years after the Big Bang, space is now cold and dark. While our horizon encompasses almost a trillion galaxies that have formed over that time, they are terribly faint, and we need our most powerful telescopes to tally their presence directly. But their stars and accreting black holes contribute in whole or part to a background of visible light that pervades the Universe. Paradoxically, it can be detected with a small telescope simply stationed at a suitable vantage point.
This cosmic optical background (COB) testifies to all processes that have generated light over the history of the Universe. Is the COB intensity as expected from our census of faint galaxies, or does the Universe contain additional sources of light not yet recognized? We have attempted to detect the COB with the Long-range Reconnaissance Imager (LORRI; Cheng et al. 2008; Weaver et al. 2020) on board NASA's New Horizons spacecraft as it explores the outer limits of the Kuiper Belt, bound for the depths of the interstellar space beyond. At 57 au from the Sun, it is the most remote camera ever deployed. And it looks out into the darkest skies ever seen.
At New Horizons' (NH) location, the sky is essentially free of the zodiacal light (ZL) foreground, which is sunlight scattered by interplanetary dust. ZL strongly dominates the sky brightness in the inner solar system and has bedeviled all attempts to measure the COB from Earth-space. Zemcov et al. (2017), however, recognized that the LORRI camera on NH could be useful for COB observations, and from the limited archival observations available at the time, they recovered an upper limit to the COB intensity somewhat lower than the low-significance COB measurements based on Hubble Space Telescope (HST), CIBER, and other observations.
Lauer et al. (2021, hereafter NH21) measured the COB from deep LORRI archival images obtained after the NH Pluto encounter. Based on seven fields at 42–45 au from the Sun, we measured the COB intensity to be in the range 15.9 ± 4.2 (1.8 stat., 3.7 sys.) nW m−2 sr−1 at the LORRI pivot wavelength of 0.608 μm. 13 When the estimated integrated light of galaxies (IGL) fainter than the LORRI photometric detection limit was subtracted from this intensity, a component of unknown origin in the range 8.8 ± 4.9 (1.8 stat., 4.5 sys.) nW m−2 sr−1 remained.
The NH21 analysis also showed that, while the strong ZL foreground was eliminated by the great distance of NH from the Sun, corrections for other foreground light sources were still required. The strongest of these was diffuse Galactic light (DGL), which is Milky Way starlight scattered into the line of sight by interstellar dust. We also had to correct for scattered starlight (SSL) from bright stars outside the LORRI field of view. DGL and SSL vary strongly over the sky, however, which means that fields can be targeted that greatly minimize the contributions of both foregrounds, compared to what is available from the random COB sampling provided by archival images observed for other purposes.
The present work is based on a program of new LORRI images obtained explicitly to minimize foreground contributions to the COB intensity observations. The program also incorporates improved understanding of how to use LORRI for low light-level imaging, as well as calibration observations obtained to improve understanding of the DGL and SSL foregrounds.
In 2021 we tested our observational strategy by imaging one of the 16 COB fields that define the present program. That test field, designated as NHTF01, verified our ability to select for greatly reduced DGL and SSL foregrounds. Its analysis yielded a highly significant detection of the COB at 16.37 ±1.47 nW m−2 sr−1 (Lauer et al. 2022, hereafter NH22). Intriguingly, the estimated intensity due to all background galaxies (IGL) accounted for only half of this signal, implying that the COB also includes an intensity component of unknown origin at 8.06 ± 1.92 nW m−2 sr−1. This conclusion was supported by an independent analysis of archival LORRI observations by Symons et al. (2023), which recovered a total COB intensity of 21.98 ± 1.83 (1.23 stat, 1.36 sys) nW m−2 sr−1, a result that implied the existence of an even larger anomalous component.
With the complete COB survey, however, we have reworked the estimation of the DGL foreground, finding its contribution to be stronger than the DGL estimates used in NH21 and NH22. This now reduces the total COB intensity estimate, and more than halves both the estimated anomalous component and its significance. While our observations can accommodate a modest COB anomaly relative to the amplitude of the IGL, we cannot falsify the simpler hypothesis that the COB is due entirely to the known population of galaxies.
Although the present paper reaches a qualitatively different conclusion about the COB than did NH21 and NH22, it does rely heavily on the analysis developed in those two earlier papers. We summarize the interrelationship of all three papers in fine detail in Table 1. The first column shows the sample selection, image analysis, and treatments of foreground components developed and presented in NH21, with the sections of that paper identified where the given item was discussed in detail. The second column shows where NH22 augments or revises the analysis details in NH21. The final column shows where the present paper augmented or revised our previous works.
Table 1. The New Horizons Cosmic Optical Background Program
| NH21 (Lauer et al. 2021) | NH22 (Lauer et al. 2022) | This Work |
|---|---|---|
| Sample Selection: Section 2 SEA ≥ 95° | ||
| Section 2 Delay 150 s | ||
| Section 2 Gal. lat. ∣b∣ ≥ 50° | Section 2.1 Gal. lat. ∣b∣ ≥ 40° | |
| Section 2 Exp. time 30 s | Section 2.2 Exp. time 65 s | |
| Section 2 Number of fields: 7 | Section 2.1 Number of fields: 1 | Section 2.1 Number of fields: 16 + 8 DCAL |
| Section 2.1 Minimize DGL, SSL for field selection | ||
| Single image detection limit: Section 4.2 V = 19.1 | Section 2.4 V = 19.9 | |
| Environment: Section 2.1 Spacecraft shadow | ||
| Section 2.1.1 Thruster exhaust | ||
| Appendix A.1 Cherenkov (RTG γ-rays) | ||
| Appendix A.2 Fluorescence (RTG γ-rays) | ||
| Appendix A.3 Cherenkov (RTG scattered γ-rays) | ||
| Appendix A.4 Cherenkov (RTG neutrons) | ||
| Appendix A.5 Cherenkov (cosmic rays) | ||
| Image Analysis: Section 2.1 Power-on fade | ||
| Section 3.1.1 Bias level | ||
| Section 3.1.2 Dark current | ||
| Section 3.1.3 Bias structure | ||
| Section 3.1.3 Jail bars | ||
| Section 3.1.4 Charge smear | ||
| Section 3.1.4 Flat fielding | ||
| Section 3.2.1 Object masking | ||
| Section 3.2.2 Sky measurement | ||
| Section 2.3 A/D correction | Section 2.2 No A/D correction needed | |
| Section 2.5 Background decay | ||
| Foregrounds: Section 4.3 Scattered starlight | ||
| Section 4.1 Integrated starlight | ||
| Section 4.2 Integrated galaxy light | ||
| Section 4.3 SGL = 0.07 nW m−2 sr−1 | Section 4.3 SGL = 0.10 nW m−2 sr−1 | |
| Section 3.7 Bright galaxies (PS1) | Section 3.1 Bright galaxies (DLS) | |
| Section 3.4 Two-photon continuum (2PC) | Section 3.4 No 2PC correction needed | |
| Section 3.4 Hα emission (WHAM) | ||
| DGL: Section 4.4 FIR band 100 μm (IRIS) | Section 4.3 FIR 350 μm + 550 μm (Planck) | |
Section 4.4 FIR aperture 0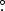 2 radius circle 2 radius circle | Section 4.2 FIR aperture LORRI FOV | |
| Section 4.4.1 Residual ZL correction (error) | Section 4 No residual ZL correction needed | |
| Section 4.4 Estimator: Zemcov; Brandt & Draine | Section 3.2 Zemcov only | Section 4.3 NCOB + DCAL self-calibration |
Note. The first column lists the major components of the COB measurement presented in NH21 (cross-referenced by the section in the paper in which it was discussed). The second column shows where the second paper, NH22, introduced new major components (those with no previous NH21 entry) or revised the analysis in NH21 (a previous NH21 entry was given). The final column shows how the present paper revised or augmented the analysis present in NH22 and/or NH21. We marked the NH21 residual ZL correction entry with "error" as its use in NH21 and NH22 was incorrect. A blank column entry to the right of a filled column entry means no change was made from the previous work.
Download table as: ASCIITypeset image
2. The COB Survey
2.1. The Survey Design and Field Selection
A truly cosmological optical background should present no more structure than would be expected given the known projected correlation function of large-scale structure marked by galaxies over the age of the Universe. More plainly, we expect the field-to-field variation of observed COB intensity to be more or less isotropic, once known instrumental effects and Galactic foregrounds have been corrected for. An ideal COB survey would attempt to uniformly sample the full sky on all angular scales. However, foregrounds associated with the Milky Way, or even the solar system, are markedly anisotropic over large angular scales. Thus any realistic survey will have additional Galactic and ecliptic coordinate constraints to minimize those foregrounds. Within such constraints, however, we are free to identify survey areas that specifically minimize both the DGL and SSL foregrounds, which are the two dominant foreground signatures for our observing platform.
In the case of the present survey, several considerations limit us to observing in somewhat restricted regions close to the Galactic poles. The strongest restriction is that needed to avoid scattered sunlight entering the LORRI aperture. This issue is discussed in detail in NH21; briefly, we require the aperture to be fully in the shadow of the NH spacecraft. This requirement means selecting fields with solar elongation angle (SEA) > 95°. While SEA > 90° would be sufficient to keep direct sunlight out of the LORRI aperture, the spacecraft bulkhead in which the aperture is positioned also supports other instruments that could potentially scatter sunlight into LORRI; SEA > 95° ensures that these are also shaded by the spacecraft (Weaver et al. 2020; NH21).
The trajectory of NH out of the solar system was completely specified by its primary mission of obtaining the first exploration of Pluto (Stern et al. 2015) and the Kuiper belt object Arrokoth (Stern et al. 2019). At the time of the mission, Pluto as seen from Earth was projected against the bulge of the Milky Way. This means that the "antisolar" hemisphere accessible to NH is roughly centered on the heart of our galaxy. Requiring Galactic latitude ∣b∣ > 40° to avoid dense stellar foregrounds and strong dust absorption thus eliminates a significant fraction of this hemisphere. Lastly, we restrict ecliptic latitude to ∣β∣ > 15°. While NH is not directly affected by ZL, the far-infrared (FIR) intensities that we use to select COB fields are provided by maps made in Earth-space, and thus may incur larger errors near the ecliptic (Matsuura et al. 2011; Carleton et al. 2022; Korngut et al. 2022).
The combination of these three constraints (SEA > 95°, ∣b∣ > 40°, and ∣β∣ > 15°) leaves 4239 deg2 of sky available. We randomly selected 60,000 positions within this area, and for each one estimated the DGL contribution using the Improved Reprocessing of the IRAS Survey (IRIS) 100 μm all-sky data and the amount of SSL entering the LORRI field of view. The details of how we derived these preliminary foreground light estimates are discussed in NH22 (see Section 2.1 of that work). We then ranked each position by the sum of these two foreground contributions and selected the 500 positions with the smallest sums for further review. From these 500 positions, we reduced the sample to 15 fields, to ensure we could perform the desired observations within the available spacecraft fuel constraints. We also ensured that there was coverage in both Galactic hemispheres and that the pointings spanned a broad range in Galactic longitude. The final coordinates of each field were adjusted by up to 0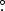 7 to minimize the presence of bright galaxies or galaxy clusters within the LORRI field of view.
14
We also used the NH22 test field (NHTF01) as part of the survey since, by definition, it meets all the above requirements. This brings the total number of COB survey fields to 16. With the exception of NHTF01, we denote the COB science fields with the prefix NCOB.
7 to minimize the presence of bright galaxies or galaxy clusters within the LORRI field of view.
14
We also used the NH22 test field (NHTF01) as part of the survey since, by definition, it meets all the above requirements. This brings the total number of COB survey fields to 16. With the exception of NHTF01, we denote the COB science fields with the prefix NCOB.
We selected an additional set of eight fields to perform an improved self-calibration of the relation of FIR intensity to optical DGL. The calibration fields for the FIR–DGL relation are denoted with the prefix DCAL. The DCAL fields were explicitly selected to cover fields with progressively higher 100 μm surface brightness, up to a limit of ∼3 MJy sr−1. This limit was selected to avoid dust optical depths large enough that nonlinear behavior between the FIR intensity and scattered light amplitude might start to come into play. All DCAL fields were selected to have SSL levels in a narrow range (6 < SSL < 9 nW m−2 sr−1) that was similar to the NCOB science fields.
We also selected eight fields to help verify the SSL estimates. These fields are denoted with the prefix SCAL. The SCAL fields were chosen to be closer to brighter stars than we would otherwise permit for the science observations to test the reliability of the scattered light estimates. All SCAL fields were selected to have DGL levels in a narrow range (3 < DGL < 6 nW m−2 sr−1) that is similar to that in the NCOB science fields.
Lastly, we selected four fields at low ecliptic latitude (∣β∣ ≤ 6°) solely to verify the lack of significant brightness from interplanetary dust (IPD) at the large heliocentric distance of the NH spacecraft at the time of our observations. These four fields are denoted with the prefix IPDF.
The coordinates, observation dates, and spacecraft heliocentric distance for the 16 COB fields, 16 calibration fields, and four IPD fields are listed in Table 2. The mission elapsed time (MET) image identifiers of the first image of each field are also given. We show the field distribution on the sky with respect to the IRIS 100 μm map in Figure 1. The  regions of sky from the DESI/DECam Legacy Survey (Dey et al. 2019, hereafter DLS) centered on our 16 COB science fields are shown in Figure 2. The intentional lack of bright optical sources in any of the fields is clearly demonstrated. Table 3 provides the Galactic extinction E(B − V), H i column density, Hα emission, dust temperature, and the FIR and cosmic IR background (CIB) intensities for each field. The CIB-subtracted FIR intensities are used to estimate the DGL foregrounds for each field. While we list the E(B − V) (Schlafly & Finkbeiner 2011) values for each field in Table 3 these extinction indicators are not used in any of the analyses in this work. Shull & Panopoulou (2024) have demonstrated that these E(B − V) values are, on average, 12% lower than those derived from Planck FIR observations. All errors listed are 1σ values.
regions of sky from the DESI/DECam Legacy Survey (Dey et al. 2019, hereafter DLS) centered on our 16 COB science fields are shown in Figure 2. The intentional lack of bright optical sources in any of the fields is clearly demonstrated. Table 3 provides the Galactic extinction E(B − V), H i column density, Hα emission, dust temperature, and the FIR and cosmic IR background (CIB) intensities for each field. The CIB-subtracted FIR intensities are used to estimate the DGL foregrounds for each field. While we list the E(B − V) (Schlafly & Finkbeiner 2011) values for each field in Table 3 these extinction indicators are not used in any of the analyses in this work. Shull & Panopoulou (2024) have demonstrated that these E(B − V) values are, on average, 12% lower than those derived from Planck FIR observations. All errors listed are 1σ values.
Figure 1. The locations of the NCOB, DCAL, SCAL, and IPD fields are shown on the IRIS full-sky 100 μm map in Galactic coordinates.
Download figure:
Standard image High-resolution imageFigure 2. The positions of the NCOB fields are shown with respect to images from the Deep Legacy Survey (Dey et al. 2019). The DLS image cutouts above show a 30' field of view centered on the LORRI position. The blue boxes show the LORRI CCD orientation relative to J2000 equatorial coordinates. The streak in the NHTF01 DLS image is an artifact. Some fields were rolled in position angle to minimize spacecraft maneuvers.
Download figure:
Standard image High-resolution imageTable 2. Survey Field Centers and Observations
| Field | R.A. (J2000) Decl. | Galactic | Galactic | Ecliptic | rh | Date | MET | |
|---|---|---|---|---|---|---|---|---|
| ID | (deg) | (deg) | Longitude | Latitude | Latitude | (au) | (UT) | (s) |
| NHTF01 | 0.0756 | −21.5451 | 55.794 | −77.094 | −19.720 | 51.3 | 2021-09-24 | 0494832182 |
| NCOB01 | 358.4334 | −54.9137 | 319.728 | −60.293 | −48.117 | 57.0 | 2023-09-14 | 0556982941 |
| NCOB02 | 5.3540 | −55.6590 | 311.662 | −60.958 | −51.123 | 56.9 | 2023-08-31 | 0555788941 |
| NCOB03 | 353.7867 | −49.1893 | 331.516 | −63.490 | −41.781 | 56.8 | 2023-08-22 | 0554999401 |
| NCOB04 | 8.0987 | −44.4906 | 314.112 | −72.222 | −43.074 | 56.8 | 2023-08-21 | 0554933281 |
| NCOB05 | 10.7611 | −27.3461 | 25.794 | −88.122 | −29.172 | 56.8 | 2023-08-29 | 0555599521 |
| NCOB06 | 9.4350 | −34.7328 | 323.189 | −81.850 | −35.192 | 57.0 | 2023-09-13 | 0556884241 |
| NCOB07 | 19.0398 | −26.6161 | 209.027 | −84.464 | −31.807 | 56.8 | 2023-08-28 | 0555537901 |
| NCOB08 | 336.2651 | −30.0473 | 18.925 | −57.870 | −18.712 | 56.9 | 2023-08-30 | 0555723121 |
| NCOB09 | 6.7398 | −22.1689 | 73.341 | −82.551 | −22.919 | 56.9 | 2023-08-30 | 0555661141 |
| NCOB10 | 15.7115 | −18.8994 | 141.203 | −81.364 | −23.521 | 56.8 | 2023-08-27 | 0555476401 |
| NCOB11 | 10.6266 | −15.2837 | 112.541 | −77.975 | −18.216 | 56.8 | 2023-08-27 | 0555414901 |
| NCOB12 | 207.4692 | 3.9649 | 336.539 | 62.959 | 14.270 | 56.8 | 2023-08-17 | 0554613781 |
| NCOB13 | 211.9528 | 4.6995 | 345.372 | 61.111 | 16.557 | 56.8 | 2023-08-17 | 0554548681 |
| NCOB14 | 356.2651 | 15.5111 | 100.270 | −44.420 | 15.684 | 56.8 | 2023-08-20 | 0554838541 |
| NCOB15 | 247.9273 | 55.2059 | 84.133 | 41.702 | 74.534 | 56.7 | 2023-08-13 | 0554210281 |
| DCAL01 | 17.0453 | −34.9907 | 279.471 | −81.361 | −38.437 | 56.8 | 2023-08-20 | 0554871721 |
| DCAL02 | 21.3854 | −36.2819 | 266.706 | −78.332 | −41.288 | 57.0 | 2023-09-12 | 0556822921 |
| DCAL03 | 239.1696 | 44.8625 | 71.217 | 49.235 | 62.786 | 56.7 | 2023-08-13 | 0554274001 |
| DCAL04 | 243.8895 | 52.4461 | 81.173 | 44.640 | 70.921 | 56.7 | 2023-08-13 | 0554242381 |
| DCAL05 | 236.0924 | 34.9450 | 55.856 | 52.438 | 52.762 | 56.7 | 2023-08-14 | 0554305561 |
| DCAL06 | 36.3653 | −58.9600 | 282.325 | −54.245 | −65.192 | 57.0 | 2023-09-13 | 0556916881 |
| DCAL07 | 228.2392 | 24.1691 | 35.663 | 58.073 | 40.267 | 56.7 | 2023-08-15 | 0554368501 |
| DCAL08 | 235.2073 | 24.5594 | 38.839 | 51.978 | 42.723 | 56.7 | 2023-08-14 | 0554337061 |
| SCAL01 | 6.8703 | −33.6610 | 339.789 | −81.676 | −33.240 | 57.0 | 2023-09-12 | 0556790881 |
| SCAL02 | 344.2125 | −42.5989 | 351.834 | −62.077 | −32.811 | 57.0 | 2023-09-12 | 0556783201 |
| SCAL03 | 346.2247 | −43.7754 | 348.135 | −62.860 | −34.496 | 57.0 | 2023-09-12 | 0556786801 |
| SCAL04 | 7.1526 | −43.8832 | 316.818 | −72.624 | −42.197 | 57.0 | 2023-09-11 | 0556781041 |
| SCAL05 | 245.6015 | 54.3330 | 83.387 | 43.205 | 73.058 | 56.7 | 2023-08-12 | 0554149081 |
| SCAL06 | 345.0136 | −43.5540 | 349.450 | −62.190 | −33.892 | 57.0 | 2023-09-12 | 0556785001 |
| SCAL07 | 10.7746 | −46.1545 | 307.349 | −70.902 | −45.497 | 57.0 | 2023-09-11 | 0556770781 |
| SCAL08 | 345.8313 | −48.0810 | 340.769 | −60.336 | −38.144 | 57.0 | 2023-09-12 | 0556788661 |
| IPDF01 | 4.9830 | 2.6940 | 107.415 | −59.225 | 0.493 | 56.8 | 2023-08-19 | 0554765221 |
| IPDF02 | 8.8178 | 4.6502 | 115.318 | −57.982 | 0.780 | 56.8 | 2023-08-19 | 0554767681 |
| IPDF03 | 9.6595 | −1.8759 | 115.469 | −64.562 | −5.552 | 56.8 | 2023-08-19 | 0554762701 |
| IPDF04 | 4.9272 | −4.3385 | 103.170 | −65.985 | −5.939 | 56.8 | 2023-08-19 | 0554760181 |
Note. All coordinates are in degrees. The rh parameter is the distance of the spacecraft from the Sun at the time of the observation. MET is the mission elapsed time in seconds of the first image in each field sequence. NCOB fields are the primary fields for measuring the COB intensity. NHTF01 is the test of the NCOB field selection and observational strategy published earlier in NH22. DCAL and SCAL fields are for DGL and scattered starlight calibration, respectively. IPD fields are the low-ecliptic-latitude fields taken to verify the lack of zodiacal emission at these large heliocentric distances.
Download table as: ASCIITypeset image
Table 3. Field Properties for Dust, Gas, and FIR Emission
| Field | E(B − V) | N(H i) | Hα | TDust | I(350 μm) | CIB (350 μm) | I(550 μm) | CIB (550 μm) |
|---|---|---|---|---|---|---|---|---|
| ID | (mag) | (1020 cm−2) | (R) | (K) | (MJy sr−1) | (MJy sr−1) | (MJy sr−1) | (MJy sr−1) |
| NHTF01 | 0.014 | 1.613 | 0.517 ± 0.035 | 21.73 ± 0.04 | 0.918 ± 0.046 | 0.521 ± 0.035 | 0.450 ± 0.023 | 0.343 ± 0.010 |
| NCOB01 | 0.007 | 1.040 | 0.705 ± 0.041 | 17.31 ± 0.03 | 0.799 ± 0.040 | 0.451 ± 0.034 | 0.390 ± 0.020 | 0.303 ± 0.009 |
| NCOB02 | 0.008 | 1.259 | 0.783 ± 0.042 | 17.79 ± 0.04 | 1.053 ± 0.053 | 0.632 ± 0.034 | 0.503 ± 0.025 | 0.398 ± 0.009 |
| NCOB03 | 0.008 | 1.083 | 0.867 ± 0.045 | 17.91 ± 0.03 | 0.934 ± 0.047 | 0.565 ± 0.034 | 0.459 ± 0.023 | 0.370 ± 0.009 |
| NCOB04 | 0.005 | 3.337 | 1.017 ± 0.047 | 16.93 ± 0.03 | 0.824 ± 0.041 | 0.557 ± 0.034 | 0.426 ± 0.021 | 0.355 ± 0.009 |
| NCOB05 | 0.008 | 1.222 | 0.428 ± 0.039 | 20.75 ± 0.02 | 0.975 ± 0.049 | 0.677 ± 0.034 | 0.499 ± 0.025 | 0.429 ± 0.009 |
| NCOB06 | 0.010 | 1.908 | 0.646 ± 0.042 | 20.20 ± 0.02 | 0.978 ± 0.049 | 0.585 ± 0.034 | 0.471 ± 0.024 | 0.376 ± 0.009 |
| NCOB07 | 0.011 | 1.348 | 0.324 ± 0.035 | 20.70 ± 0.06 | 1.001 ± 0.050 | 0.574 ± 0.034 | 0.485 ± 0.024 | 0.374 ± 0.009 |
| NCOB08 | 0.013 | 1.045 | 0.693 ± 0.039 | 21.53 ± 0.07 | 0.913 ± 0.046 | 0.578 ± 0.034 | 0.456 ± 0.023 | 0.370 ± 0.009 |
| NCOB09 | 0.013 | 1.440 | 0.549 ± 0.035 | 22.82 ± 0.03 | 1.014 ± 0.051 | 0.647 ± 0.035 | 0.500 ± 0.025 | 0.406 ± 0.010 |
| NCOB10 | 0.012 | 1.143 | 0.314 ± 0.034 | 23.01 ± 0.15 | 0.912 ± 0.046 | 0.628 ± 0.034 | 0.481 ± 0.024 | 0.399 ± 0.009 |
| NCOB11 | 0.012 | 1.396 | 0.390 ± 0.034 | 24.03 ± 0.01 | 0.853 ± 0.043 | 0.534 ± 0.034 | 0.420 ± 0.021 | 0.350 ± 0.009 |
| NCOB12 | 0.019 | 1.833 | 0.408 ± 0.032 | 20.59 ± 0.02 | 1.243 ± 0.062 | 0.535 ± 0.034 | 0.567 ± 0.028 | 0.349 ± 0.009 |
| NCOB13 | 0.020 | 1.916 | 0.452 ± 0.033 | 21.14 ± 0.01 | 1.204 ± 0.060 | 0.581 ± 0.034 | 0.543 ± 0.027 | 0.371 ± 0.009 |
| NCOB14 | 0.017 | 2.213 | 0.973 ± 0.033 | 18.57 ± 0.08 | 1.357 ± 0.068 | 0.524 ± 0.034 | 0.591 ± 0.030 | 0.335 ± 0.009 |
| NCOB15 | 0.005 | 1.502 | 0.459 ± 0.036 | 17.60 ± 0.06 | 0.890 ± 0.045 | 0.554 ± 0.034 | 0.460 ± 0.023 | 0.357 ± 0.009 |
| DCAL01 | 0.016 | 1.770 | 0.484 ± 0.043 | 20.91 ± 0.01 | 1.194 ± 0.060 | 0.668 ± 0.034 | 0.584 ± 0.029 | 0.419 ± 0.009 |
| DCAL02 | 0.019 | 1.947 | 0.975 ± 0.057 | 20.90 ± 0.02 | 1.195 ± 0.060 | 0.552 ± 0.034 | 0.551 ± 0.028 | 0.368 ± 0.009 |
| DCAL03 | 0.017 | 1.466 | 0.740 ± 0.035 | 19.50 ± 0.07 | 1.138 ± 0.057 | 0.530 ± 0.035 | 0.519 ± 0.026 | 0.351 ± 0.010 |
| DCAL04 | 0.019 | 1.751 | 0.633 ± 0.034 | 19.03 ± 0.02 | 1.361 ± 0.068 | 0.569 ± 0.034 | 0.607 ± 0.030 | 0.369 ± 0.009 |
| DCAL05 | 0.024 | 2.021 | 0.698 ± 0.034 | 20.73 ± 0.02 | 1.387 ± 0.069 | 0.615 ± 0.034 | 0.596 ± 0.030 | 0.390 ± 0.009 |
| DCAL06 | 0.028 | 2.951 | 0.886 ± 0.053 | 19.43 ± 0.02 | 1.808 ± 0.090 | 0.545 ± 0.034 | 0.770 ± 0.039 | 0.364 ± 0.009 |
| DCAL07 | 0.037 | 3.557 | 0.812 ± 0.039 | 18.78 ± 0.01 | 2.044 ± 0.102 | 0.488 ± 0.034 | 0.832 ± 0.042 | 0.327 ± 0.009 |
| DCAL08 | 0.038 | 3.646 | 0.852 ± 0.033 | 19.78 ± 0.01 | 2.047 ± 0.102 | 0.545 ± 0.034 | 0.843 ± 0.042 | 0.355 ± 0.009 |
| SCAL01 | 0.010 | 1.197 | 0.604 ± 0.044 | 19.68 ± 0.07 | 0.911 ± 0.046 | 0.606 ± 0.035 | 0.460 ± 0.023 | 0.386 ± 0.010 |
| SCAL02 | 0.008 | 1.006 | 0.919 ± 0.046 | 19.07 ± 0.05 | 0.935 ± 0.047 | 0.581 ± 0.034 | 0.472 ± 0.024 | 0.378 ± 0.009 |
| SCAL03 | 0.010 | 0.882 | 0.762 ± 0.043 | 17.94 ± 0.01 | 0.901 ± 0.045 | 0.556 ± 0.034 | 0.446 ± 0.022 | 0.355 ± 0.009 |
| SCAL04 | 0.009 | 1.805 | 0.723 ± 0.043 | 16.88 ± 0.01 | 0.953 ± 0.048 | 0.629 ± 0.034 | 0.470 ± 0.024 | 0.393 ± 0.009 |
| SCAL05 | 0.007 | 1.133 | 0.290 ± 0.035 | 18.05 ± 0.08 | 0.903 ± 0.045 | 0.541 ± 0.034 | 0.451 ± 0.023 | 0.350 ± 0.009 |
| SCAL06 | 0.008 | 0.946 | 0.868 ± 0.043 | 18.28 ± 0.03 | 0.889 ± 0.044 | 0.550 ± 0.034 | 0.451 ± 0.023 | 0.360 ± 0.009 |
| SCAL07 | 0.010 | 2.384 | 0.688 * | 17.83 ± 0.03 | 1.015 ± 0.051 | 0.634 ± 0.034 | 0.495 ± 0.025 | 0.397 ± 0.009 |
| SCAL08 | 0.009 | 0.997 | 0.825 ± 0.044 | 18.22 ± 0.06 | 0.968 ± 0.048 | 0.618 ± 0.034 | 0.470 ± 0.024 | 0.395 ± 0.009 |
| IPDF01 | 0.020 | 3.038 | 0.561 ± 0.036 | 18.69 ± 0.04 | 1.355 ± 0.068 | 0.498 ± 0.034 | 0.587 ± 0.029 | 0.326 ± 0.009 |
| IPDF02 | 0.021 | 2.972 | 0.478 ± 0.034 | 18.98 ± 0.03 | 1.539 ± 0.077 | 0.612 ± 0.034 | 0.674 ± 0.034 | 0.393 ± 0.009 |
| IPDF03 | 0.020 | 2.257 | 0.539 ± 0.042 | 20.77 ± 0.04 | 1.295 ± 0.065 | 0.566 ± 0.034 | 0.552 ± 0.028 | 0.360 ± 0.009 |
| IPDF04 | 0.019 | 2.311 | 0.420 ± 0.044 | 21.15 ± 0.00 | 1.320 ± 0.066 | 0.616 ± 0.034 | 0.595 ± 0.030 | 0.390 ± 0.009 |
Note. E(B − V) values are from Schlafly & Finkbeiner (2011) obtained via the IPAC website. H i column densities are from the HI4PI survey (HI4PI Collaboration et al. 2016). Hα values are from the WHAM survey (Haffner et al. 2003). The Hα value for SCAL07 is contaminated by a nearby bright star. Dust temperatures are from Irfan et al. (2019) and are derived using IRAS and Planck observations. FIR intensities and CIB measurements are based on Planck HFI observations (Planck Collaboration et al. 2020). FIR intensity values are the mean value within the LORRI field of view for the indicated target field. The CIB level has not been subtracted from the FIR intensity values given in columns (6) and (8). The CIB values given here are the mean values within the same LORRI FOV derived from the CIB maps created using the generalized needlet internal linear combination (GNILC) method (Planck Collaboration et al. 2016b) for the indicated passband. We add to the zero-offset CIB GNILC maps the relevant monopole level from Odegard et al. (2019).
Download table as: ASCIITypeset image
2.2. Images of the Fields
Images of the survey fields were obtained with LORRI. With the exception of those for NHTF01, the observations were obtained over August and September of 2023 when the spacecraft was nearly 57 au from the Sun. For each COB survey field (those designated with the NCOB prefix), 16 LORRI exposures of 65 s each were obtained, while eight exposures of 65 s were obtained of the DGL calibration (DCAL) and scattered starlight calibration (SCAL) fields. The imaging sequences for each of the four IPD fields consisted of 16 LORRI exposures of 65 s each. To avoid the LORRI "background fade" anomaly associated with the activation of the camera (NH21), no images were obtained earlier than four minutes after LORRI was powered on.
LORRI is an unfiltered (white light) 1032 × 1024 pixel CCD imager mounted on a 20.9 cm aperture Cassegrain reflector. The active imaging area is 1024 × 1024 pixels, with the final eight columns being covered by a dark shield. The last four shielded columns are used to measure the combined dark current and electronic bias level. For deep observations, such as those used for COB measurements, the camera is operated with 4 × 4 pixel binning, producing raw images in 257 × 256 pixel format, including a single bias/dark column. The pixel scale in this mode is 4 08, which provides a
08, which provides a  field. LORRI's sensitivity extends from the blue (0.4 μm) to near-infrared (0.9 μm) and is defined by the CCD response and telescope optics. The pivot wavelength is 0.608 μm. The gain is 19.4e− per 1 DN, and the read noise is 24e−. In 4 × 4 mode, the photometric zero-point is 18.88 ± 0.01 AB magnitudes, corresponding to an exposure level of 1 DN s–1 (Weaver et al. 2020).
field. LORRI's sensitivity extends from the blue (0.4 μm) to near-infrared (0.9 μm) and is defined by the CCD response and telescope optics. The pivot wavelength is 0.608 μm. The gain is 19.4e− per 1 DN, and the read noise is 24e−. In 4 × 4 mode, the photometric zero-point is 18.88 ± 0.01 AB magnitudes, corresponding to an exposure level of 1 DN s–1 (Weaver et al. 2020).
The suitability of LORRI for COB observations is discussed at length in NH21 and NH22. In short, we have explored the spacecraft environment for potential extraneous contributions to the background sky level, as well as similar effects in the LORRI camera. As shown in NH21, the spacecraft shadow is adequate for preventing both direct and indirect solar illumination of the LORRI aperture. Analysis in NH21 also shows that the thrusters that control the spacecraft attitude do not generate particulates around the spacecraft that scatter sunlight. Lastly, γ-rays emitted by the spacecraft's radioisotope thermoelectric generator (RTG) or cosmic rays do not generate significant intensities of optical photons through the Cherenkov or fluorescent mechanisms (see NH22).
As LORRI is operated, the electronic bias level and average dark-current level are measured from the overscan column as a combined electronic background level. In NH21 we presented the analysis of a novel calibration sequence of exposures that allowed for direct isolation of the dark level. This demonstrated that the dark current was as expected, based on prelaunch calibration tests. In NH21 we further demonstrated that bias images obtained with LORRI produced a null background. In NH22 we discussed our discovery of a low-level error in the LORRI analog/digital conversion electronics, which caused the bias level to be in error by 0.02 DN. Subsequent analysis shows that it affects other signal measurements at the same level, thus it has no significant net effect and is ignored in the present analysis.
2.3. Image Reduction
The sky levels in the images are only slightly greater than 1 DN. Accurate recovery of the sky intensity thus requires attention to subtle effects that become important at this level. As detailed in NH21 and NH22, we use a custom image reduction pipeline to optimize accurate recovery of the faint sky signal. This includes estimating the bias level by fitting a Gaussian to the peak of the DN histogram of the bias column. We also include a special step to correct for the "jail bar" pattern, in which the bias level of the even-numbered columns in the CCD is offset by either +0.5 or −0.5 DN from that of the odd-numbered columns (the sign of the correction varies randomly between LORRI power-on cycles). Lastly, we exclude bright cosmic-ray hits and negative amplifier "undershoot" artifacts associated with overexposed stars from the LORRI charge-smear corrections, as they are not smeared.
2.4. Measuring the Sky Level
The procedures for measuring the sky levels are discussed extensively in NH21. In brief, we measure the sky for each individual exposure by first masking out foreground stars, galaxies, hot pixels, and cosmic-ray events, and then fitting a Gaussian to the peak of the intensity histogram of the remaining unmasked pixels. The histogram-fitting algorithm is designed to take into account fine-scale structure in the distribution of pixel intensity values that results from the image calibration operations applied to the initially integer raw pixel values. We emphasize that the final sky value for a given field is the the average of the individual sky levels measured for the 16 or eight images obtained of the field, as opposed to the single sky value measured from a stack of all the images. As noted in Weaver et al. (2020) and NH21, LORRI exhibits a slowly varying pattern of row-wise low-amplitude (<1 DN) streaks in its bias level. This pattern is treated as a random noise source, which is captured in the dispersion of sky values measured for any field.
2.5. Background Decay
In NH21 we discovered that images taken shortly after LORRI was powered on had elevated background levels, which appeared to decay away during the initial four minutes of operation. The cause of this background effect is unknown. The NH22 test COB images were therefore obtained only after this "cool-down" interval had elapsed following activation of the instrument. As noted in NH22, the sky levels in the 16 images obtained of the test field appeared to be constant over the sequence, validating this solution. We thus used the same procedure to obtain the present data.
Examining the sky levels measured for each image in our present richer data set, however, we have found that the background decay still continues even after the four minute delay, albeit at a low level. Comparison of the amplitude of the decaying background between the NCOB and DCAL exposures, which covers roughly a factor of two in total sky level, shows that the background excess was not tied to the exposure level. It is thus modeled as an additive effect.
All NCOB exposures comprise the same sequence of eight images of 65 s taken in rapid succession, followed by an 80 s pause to adjust the spacecraft pointing, followed by the final eight images, again taken in rapid succession. Subtracting the mean total sky level from the complete set of 16 images for any field showed that the first images had generally positive residuals compared to the average level over the sequence, with the final images having slightly negative residuals. Figure 3 shows the average residual trend for all the NCOB fields as a function of time.
Figure 3. The plot shows the average residuals in the total sky level for each image obtained for a given field, as a function of time since the sequence started, under the assumption that the sky level is constant over the sequence of images for any given field. The 15 NCOB fields (blue) each comprise 16 images, and the eight DCAL fields (red) comprise eight images. The curve is an exponential decay model fitted to the average NCOB residuals. The reference level for the DCAL residuals is taken as the average of the model over the first eight NCOB images.
Download figure:
Standard image High-resolution imageAn exponential decay model appears to be an excellent description of the behavior of the residuals with time. We fitted the trace as

where Δsky(t) is the average sky residual at any position on the NCOB exposure sequence, t is the time since the start of the sequence, and b is a constant background, which accounts for the fact that the initial mean sky for any field will include the background excess. For the NCOB sequence, a least-squares fit recovers a = 0.315 DN, τ = 295 s, and b = −0.075 DN, which corresponds to 1.72 nW m−2 sr−1 in intensity units. The background term in essence is the correction needed for the initial total sky levels to account for the presence of the decaying background. In practice, we use the model to apply a correction to each image in the sequence, which removes a source of variance in determination of the final average level, thus reducing the random error in the total sky measurements. We have also now applied this correction to NHTF01, with the caveat that its images were taken over a longer interval, thus reducing its net correction to −0.061 DN, or 1.39 nW m−2 sr−1.
The final decay model fitted to the uncorrected residuals is shown in Figure 3. We also include the sky residuals from the DCAL images in the figure. These fields have only eight images, and the shorter duration of the exposure sequence following the start of the sequence means that they are affected more strongly by the decaying background. The exponential model also provides the correction for the DCAL sky residuals, which are in excellent agreement with the residuals from the NCOB images taken at the same time lag. Use of the decay correction does add a systematic uncertainty of 0.16 nW m−2 sr−1 to the the sky level for any field, which is included in the total error budget.
3. Decomposition of the Total Sky Intensities
Given a total sky level for any field, our goal is to show whether or not we can account for all sources contributing to it. A portion of the sky should be due to the COB, and as part of the decomposition of the total sky, we will take as given the estimated IGL provided by all galaxies with the fields. A second component is the foreground light intensity contributed by the integrated faint starlight (ISL) emitted by stars within the fields fainter than the photometric limit for detecting any single star directly. We also have to account for SSL falling in the LORRI fields from bright stars outside the nominal field of view (bright galaxies outside the fields also contribute a minute amount of intensity). We also include the small contribution to the total sky from Hα emission in the local interstellar medium. Lastly, we must estimate the DGL component contributed by light from the Milky Way scattered by dust in the interstellar medium into our line of sight. The COB is then defined to be the IGL estimate plus any anomalous intensity left over from this decomposition that cannot be attributed to a known source.
We do the decomposition in two steps. The IGL, ISL, and SSL intensities are specified by external information, as discussed in detail in NH21 and NH22. For convenience, we also provide brief summaries of these components in the subsections that follow. In passing, we also discuss the hydrogen "two-photon" continuum correction that we included in NH22 but subsequently concluded was not needed. Subtraction of the IGL, ISL, and SSL intensities from the total skies leaves the DGL and any anomalous component, which we then disentangle in a second step, as will be discussed in the following section.
3.1. Integrated Galaxy Light
We compute the total IGL in two steps: the bright IGL (hereafter BIGL) for galaxies with V < 19.9 that were masked during the sky estimation process and the faint IGL for galaxies below this LORRI detection threshold. The IGL for the bright galaxies (V < 19.9) is estimated by extracting nonstellar objects in our LORRI field of view from the DLS DR10 (Dey et al. 2019). We use NOIRLab's Astro Data Lab interface for retrieving the galaxy catalogs. The transformation to V-mag from the DLS g and r bands (or the g and i bands when the r band is unavailable) is derived from eight templates of galaxy spectral energy distributions spanning the morphology types E, S0, Sa, Sb, Sc, and Ir. We weight the templates by the morphological fractions observed in the field population of galaxies and derive an average (V − g) versus (g − r) relationship (or versus (g − i) when r-band information is unavailable) over the redshift range 0 < z ≤ 1, typical for brighter galaxies. Our best-fit color transformations are

These relations are valid over the ranges 0.6 ≤ (g − r) ≤ 1.5 and 0.4 ≤ (g − i) ≤ 2.8. We then derive the IGL intensity contribution based on the V magnitude and sum up the contributions for all DLS galaxies with V < 19.9 in the LORRI field of view. The statistical error for the bright IGL is ∼0.01 nW m−2 sr−1 and is derived from the photometric errors given in the DLS catalogs. The systematic error for the bright IGL, typically ∼0.07 nW m−2 sr−1, is derived from the uncertainties associated with the color transformation to the V band. As noted in Table 1, the BIGL addition for galaxies brighter than the LORRI detection limit was not applied in our NH21 analysis but was applied in NH22 and is applied in this work. The typical BIGL component for the fields used in NH21 is ∼1.2 nW m−2 sr−1.
The precepts for estimating the faint IGL due to galaxies at or below the V = 19.9 detection threshold are discussed at length in NH21. We estimate the uncertainty in the faint IGL intensity by assessing the specific contribution to the error from the systematic terms (errors in the fits to the galaxy number counts) and from the statistical errors (cosmic variance). The two systematic errors associated with the fits to the galaxy number counts are from the errors in the coefficients to the power-law fits used in NH21 and the error associated with the form of the fitting function. The formal errors in the power-law coefficients yield a fractional error of 13.1% in the IGL intensity. The difference between the IGL derived from the power-law fits and that derived using a quadratic fit to the galaxy counts yields a fractional change in the IGL of 6.6%. Summing these two error components in quadrature yields a combined systematic fractional error of 14.7% in the IGL intensity. The total error in the IGL must also include the statistical uncertainty due to the effects of cosmic variance over a single LORRI field of view (FOV). The cosmic variance error for a single LORRI FOV used in this work is the same as the single-field cosmic variance error adopted in NH21 (Trenti & Stiavelli 2008), which translates to an IGL fractional error of 11.8%. Summing, in quadrature, this statistical error with the above systematic error yields a total fractional error of 18.8% in the faint IGL intensity. Combining the bright and faint galaxy contributions to the IGL gives a total IGL intensity for each of our survey fields. This IGL corresponds to the expected light in the LORRI bandpass from all galaxies brighter than V = 30 mag. The bright and faint IGL values and their associated total errors are provided in Table 4 for each field.
3.2. Scattered Light from Bright Stars and Galaxies (SSL and SGL)
The LORRI instrument accepts scattered starlight from sources well outside its field of view. The NCOB fields were selected to minimize SSL, and the SSL intensity remaining for any given field depends on the specific stars that surround it. As detailed in NH21, the LORRI scattered light function is estimated from prelaunch calibration tests and from in-flight measurements of the scattered sunlight background as a function of angular distance from the Sun. The SSL is estimated from the convolution of the scattering function with stars surrounding the field as provided by the Tycho2 star catalog (Høg et al. 2000), and the Yale Bright Star catalog v5.0 (Hoffleit & Warren 1995) for bright stars, with fainter stars (11 mag ≤ V < 20 mag) provided by the Gaia DR3 catalog (Gaia Collaboration et al. 2016, 2023). The error in the SSL intensity reflects the 10% scatter in the LORRI scattering function, and thus is systematic over all fields. We used the Gaia ESA Archive to retrieve all of the above star catalogs for each field. The SSL values for each field are given in Table 4.
The scattered galaxy light (SGL) term is the analogous scattered light contributed by bright galaxies outside the LORRI field. As with the SSL calculation, the contribution to the SGL is calculated out to an off-axis angle of 45°. Because no uniform all-sky galaxy catalog yet exists to perform this calculation using the actual positions and fluxes of known galaxies, we estimate the SGL as described in NH21. Briefly, we use the galaxy number counts from well-calibrated surveys to compute the mean surface brightness of galaxies with V < 20 and then compute the contribution to each annular bin extending out to a radius of 45°. The flux contributions in each bin are convolved with the LORRI scattering function and are then summed up to provide the final SGL estimate. The same SGL value is adopted for all fields. The surface density of bright galaxies is so low that this intensity, 0.10 ± 0.01 nW m−2 sr−1, is almost negligible. Hence, even using actual galaxy positions and brightnesses would not make a substantial difference in the final results. As with the SSL, the uncertainty in SGL is taken to be 10%.
As noted in Section 2.1, we observed eight "SCAL" calibration fields to test the SSL corrections. Figure 4 shows the predicted SSL corrections for the NCOB and SCAL fields as compared to the inferred SSL corrections estimated by subtracting all other intensity components from the total observed sky intensity. In detail, this means subtracting the field-specific IGL, SGL, ISL, and Hα components discussed in this section, as well as the DGL corrections (which will be discussed in the following section), such that SSLinf =TotSky − IGL − ISL − Hα − DGL − SU. Note that we also subtracted the small anomalous SU intensity component. This is constant over all fields, and will be discussed in detail in Section 5.
Figure 4. The inferred SSL as a function of the predicted SSL for the 16 COB fields (blue points) and the eight SCAL fields (orange points). The predicted SSL is the intensity derived using the LORRI large-angle point-spread function convolved with known stars from various catalogs. The inferred SSL is the residual signal when all other non-SSL intensity components are subtracted from the total observed sky intensity. A log–log scale is used as the SSL error is proportional to the SSL signal. The dashed line shows the line of equality. The three outlier SCAL fields all have more than one V < 9.2 star (intentionally) located within 0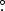 32 of the center of the LORRI field.
32 of the center of the LORRI field.
Download figure:
Standard image High-resolution imageAs is seen in the figure, there is excellent agreement between the predicted and inferred SSL intensities for the 16 NCOB fields. The three SCAL fields with the largest predicted SSL values, however, have relatively much smaller inferred SSL values. These fields were selected to return strong SSL backgrounds by positioning the LORRI FOV close to bright stars. The implication is that the scattered light function ≲0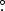 5 radii from the LORRI field overestimates the scattered light contribution. In contrast, the NCOB fields were positioned to avoid angularly close bright stars; the fainter stars remaining close to those fields contribute little to the total SSL integral. Likewise, the five SCAL fields with the smaller predicted SSL intensities also agree well with their corresponding inferred SSL backgrounds.
5 radii from the LORRI field overestimates the scattered light contribution. In contrast, the NCOB fields were positioned to avoid angularly close bright stars; the fainter stars remaining close to those fields contribute little to the total SSL integral. Likewise, the five SCAL fields with the smaller predicted SSL intensities also agree well with their corresponding inferred SSL backgrounds.
Based on the SCAL data, we do not see a strong case for changing the present SSL estimation procedure, which appears to work well for the SSL intensity range experienced by our NCOB and DCAL fields. Comparing the predicted and inferred SSL values directly for the 16 NCOB fields, we find the rms relative difference between the two values to be 15%. As the error in the inferred SSL values strongly dominates in this comparison, it means that the error in the predicted SSL value must be yet smaller. The five SCAL fields close to the equality line in Figure 4 in aggregate have markedly higher SSL backgrounds than do the NCOB fields, but here the rms relative difference between the inferred and predicted SSL values rises only slightly to 18%.
3.3. Integrated Faint Starlight
ISL is the integrated light of faint Galactic stars within any field that are fainter than the LORRI photometric detection limit. Our approach is to integrate TRILEGAL models (Girardi et al. 2005, 2012) of the expected population of faint stars down to V = 30 within a 1 deg2 region centered on our fields, following the procedures presented in NH21. For the present fields, the bright limit of the intensity integral (Equation (3) in NH21) is V = 19.9. The ISL errors (Table 4) are a combination of systematic and random errors due to uncertainties in the TRILEGAL model parameters and the estimated fluctuations in the star counts, respectively. As seen in Figure 5, the TRILEGAL predictions agree very well with the actual star counts from Gaia DR3 (Gaia Collaboration et al. 2016, 2023). We thus have confidence that the use of the TRILEGAL for predicting the ISL contribution down to V = 30 is a reliable approach. The ISL values for each field are given in Table 4.
Figure 5. The left plot shows the stellar density on the sky as a function of the absolute value of Galactic latitude from Gaia DR3 and from the TRILEGAL Milky Way model simulator for each of the 32 fields in the current work plus the 7 fields from NH21. To enable the comparison with Gaia, the stellar density calculations are limited to stars in the range 10 ≤ V < 19. The right plot shows the direct comparison of star counts from Gaia vs. TRILEGAL for this same magnitude range. The dashed green line represents the line of equality.
Download figure:
Standard image High-resolution image3.4. The Two-photon Continuum and Hα Foregrounds
The existence of a full-sky diffuse Lyα background from the Milky Way (e.g., Gladstone et al. 2021) suggests that there might be associated hydrogen two-photon continuum (2PC; Spitzer & Greenstein 1951) at some sky locations. In NH22, we noted that the preliminary analysis of deep 130–180 nm UV spectra taken of NHTF01 suggested that a significant fraction of the continuum in the UV was due to 2PC. The corresponding optical intensity in the LORRI passband was estimated to be 0.93 ± 0.47 nW m−2 sr−1. Subsequent analysis of the NHTF01 UV spectra greatly reduced the likelihood that 2PC was needed to account for the observed continuum. The strongest argument against this hypothesis, however, was provided by the extremely low level of Hα emission seen over the LORRI field. As such, in contrast to the analysis in NH22, we conclude that 2PC does not contribute to the observed sky levels at anything more than a trivial level.
The generation of 2PC emission occurs during the recombination of ionized hydrogen. The associated Hα emission is a direct predictor of 2PC continuum intensity (Kulkarni 2022; Kulkarni & Shull 2023). The Hα levels seen in the COB survey fields (see Table 3) are all very low (<1 R, the rayleigh unit) based on observations made with the Wisconsin Hα Mapper (WHAM; Haffner et al. 2003). This in turn implies that any 2PC emission present should have intensity <0.1 nW m−2 sr−1. We conclude that 2PC emission is negligible in the present NCOB fields.
That said, since Hα emission is present in its own right in the LORRI fields, it will contribute directly to the observed total sky level, albeit at an exceedingly modest level. For one rayleigh of Hα emission, the associated intensity is 0.24 nW m−2 sr−1; the median Hα intensity for the NCOB and DCOB fields is about 2/3 of that (see Table 4).
4. The Diffuse Galactic Light Foreground
The approach to estimating the DGL contribution to the sky level in any field is to first estimate the amount of interstellar dust along the line of sight, and then calculate the intensity of Milky Way light that it would scatter. In NH21 and NH22, we used the DGL estimator of Zemcov et al. (2017), which uses the residual 100 μm intensity above the CIB to estimate the amount of IR cirrus in the field, and scattering theory to estimate the actual DGL scattered into the line of sight. Unfortunately, uncertainties in the needed theoretical parameters translate into large (∼40%) errors in the DGL estimates. Zemcov et al. (2017) suggested that better accuracy might be obtained by observing fields over a range of 100 μm intensity in order to derive an empirical relation between the DGL level and the FIR indicator intensity. This approach was later attempted by Symons et al. (2023) in their independent measurement of the COB intensity from NH archival LORRI observations.
As discussed in Section 2.1, we used 100 μm intensity to select both the NCOB science fields and the DCAL fields, and had planned to derive an empirical DGL estimator based on the average 100 μm intensity in any given field. In the initial phases of this work, however, we discovered an error in our previous DGL estimates. As detailed in NH21, we concluded that the IRIS 100 μm map included an amount of residual ZL, and thus derived a correction to the input 100 μm intensity as a function of ecliptic latitude of the fields (see Figure 16 of NH21). We now understand that the rise in intensity with decreasing (absolute) ecliptic latitude is due an extended zone of dust emission at high Galactic latitude that overlaps the ecliptic plane, which we simply missed in our earlier analysis. We thus no longer apply a residual ZL correction to our FIR input intensities, although we do still retain a ∣β∣ < 15° exclusion zone for COB fields, given concern with potential systematic effects in the ZL corrections. We also note that this error caused us to underestimate the amplitude of the DGL foreground in NHTF01 analyzed in NH22; we rework the decomposition of that field as part of the present analysis.
In the course of redeveloping a 100 μm-based DGL estimator, we also explored the utility of other FIR bands to predict the mass density of IR cirrus in our fields. We found that the 350 μm (857 GHz) and 550 μm (545 GHz) intensities from the Planck High Frequency Instrument (HFI; Planck Collaboration et al. 2014, 2016a) both predict the DGL foreground with significantly higher precision. Further improvements were obtained by using 350 μm and 550 μm intensities in combination. The result is a strong improvement in characterizing the amplitude of DGL in the total sky signals for any given field. We will demonstrate this at the end of this section by comparing single-band DGL estimators at 100, 350, 550, and 849 μm to the final 350 μm plus 550 μm relation. Figure 6 shows the overlay of the LORRI field of view for our 16 COB science fields on the 550 μm HFI images. While our NCOB fields were initially selected to minimize DGL based on the 100 μm emission, the 550 μm emission in each NCOB field is also very low, further confirming the selection of these fields as optimized pointings for measuring the COB.
Figure 6. The locations of the NCOB fields are shown with respect to the 545 GHz (550 μm) Planck HFI map (Planck Collaboration et al. 2020). The field of view of each HFI cutout image is 1° × 1°. The green boxes show the LORRI CCD orientation relative to Galactic coordinates.
Download figure:
Standard image High-resolution image4.1. The Use of FIR Background Intensities to Estimate DGL
Both the NCOB and DCAL fields were selected to have relatively low IR cirrus optical depth. Thus for dust at a given temperature we expect its emitted thermal FIR intensity to be linearly related to its surface density. The corresponding optical DGL intensity is thus proportional to the dust surface density, but it is moderated by a geometric factor, g(b), that accounts for changes in the scattering phase angle with Galactic latitude. In terms of the total sky, ST, and the intensity components discussed in the previous section, we define the DGL+:

where DGL+ is the optical intensity that remains in a given field after all other known signals are subtracted from the field's total sky. The terms on the right-hand side of Equation (3) are all based on the measurements made in the optical passband. We refer to this as DGL+ because it consists of the DGL signal plus any anomalous intensity from sources not currently known or considered. For a single FIR band, a DGL+ estimator can be made by performing a least-squares linear fit using as the independent variable the FIR intensity, I(λ), corrected for the cosmic background intensity at the wavelength of the FIR intensity, CIB(λ) (Symons et al. 2023). In detail:

where g(b) is the geometric scaling factor (Jura 1979; Zemcov et al. 2017), which is defined as

where b is the Galactic latitude. In this definition g(b) is normalized to be unity at ∣b∣ = 60°, and thus only describes the relative effects of latitude. The absolute conversion from FIR intensity to optical DGL is provided by the coefficient, a, in Equation (4), which is determined empirically by fitting the independent variable (g(b) × (I(λ) − CIB(λ))) to the dependent variable (ST − IGL − SSL − SGL − ISL − I(Hα)) over the combined sample of NCOB and DCAL fields. The intercept, c, provides an estimate of any anomalous intensity contribution.
4.2. FIR Intensities and the Cosmic Infrared Background
We used the Planck 2018 HFI maps (Planck Collaboration et al. 2020) available from the NASA/IPAC Infrared Science Archive (IRSA) to provide the 350, 550, and 849 μm FIR intensities. As is evident in Figure 6, the LORRI field is large enough for the FIR background to vary over its extent. We thus took care to compute the average intensity within the full LORRI field of view. Those average FIR intensities for each field are tabulated in Table 3. The errors in the FIR intensities are predominantly systematic because the ∼5% calibration uncertainties in HFI are the dominant source of uncertainty (Planck Collaboration et al. 2016a).
For the low FIR emission fields selected, the CIB and dust thermal intensities are in rough parity. As such, accurate knowledge of the CIB is critical to correctly isolating the dust thermal emission needed to estimate the optical DGL foreground. The CIB has two components. The first is effectively the "intensity monopole" or full-sky average level of the background over the sky after removing dust and other Milky Way emission sources. The second is the field-to-field variations in the background due to CIB anisotropies.
For the monopole intensities at 350, 550, and 849 μm, we draw on Odegard et al. (2019), who derive 0.576 ± 0.034, 0.371 ± 0.018, and 0.149 ± 0.017 MJy sr−1, respectively, from Planck HFI maps (Planck Collaboration et al. 2014, 2016a). Briefly, they use H i column density as an indicator of dust surface density, which for low dust optical depth is linearly correlated with FIR intensity. The CIB monopole is derived by extrapolating this relation to zero H i column density. As the CIB monopole intensities are common to all fields, the errors in the intensities are treated as systematic.
The CIB anisotropies for any field are provided by the Planck Collaboration et al. (2016b) analysis of the Planck HFI maps, which uses a form of power-spectrum analysis, referred to as the generalized needlet internal linear combination (GNILC) method, to separate the structure of the anisotropies from that of the thermal dust emission. These are treated as a field-dependent intensity correction to the overall CIB monopole. Specifically, the CIB-subtracted FIR intensity for a given field is

where I(λ) and CIBGNILC(λ) are the averages over the LORRI field from the HFI and GNLIC CIB maps hosted at IRSA, and CIB_MONOPOLE is the relevant Odegard et al. (2019) value. The anisotropy corrections, CIBGNILC(λ) + CIB_MONOPOLE, are tabulated in Table 3; the field-to-field variations of the CIB values are treated as random errors. In application, we have found that accounting for the CIB intensity anisotropies in this way removes a significant source of variance in the relations between FIR and DGL+.
Lastly, the Planck HFI did not observe at 100 μm. We thus rely on the IRIS reprocessing of the IRAS full-sky thermal-IR maps (Miville-Deschênes & Lagache 2005) for intensities at this wavelength. The CIB intensity at this wavelength is taken to be 0.78 ± 0.21 MJy sr−1 (Lagache et al. 2000).
4.3. The DGL Estimators
Figure 7 shows the four single-band DGL estimators based on 100, 350, 550, and 849 μm intensities, derived by fitting Equation (4) to the NCOB and DCAL DGL+ values (Equation (3)). The linear fit parameters are given in Table 5. The slope of the 100 μm estimator is nearly the same as that in the Zemcov et al. (2017) theoretical estimator but clearly has much smaller errors. The 350 μm and 550 μm estimators have even tighter trends, with the scatter in the 550 μm estimator nearly a factor of two smaller than that in the 100 μm estimator. In contrast, the 849 μm estimator offers the poorest performance of the four bands tested.
Figure 7. The relationships between DGL+ intensity in the NCOB and DCAL fields as a function of IRIS 100 μm, Planck HFI 350 μm, 550 μm, or 849 μm intensity averaged over the LORRI field. The CIB background intensity has been subtracted from the input FIR intensities to isolate the FIR emission from dust alone. g(b) is a function that accounts for the phase-angle dependence of the dust scattering cross section on Galactic latitude (see Equation (5)).
Download figure:
Standard image High-resolution imageTable 4. Sky Component Intensity Levels for Each NH COB and DCAL Field
| Scattered Light from | Faint | Hα | Diffuse | Faint | Bright | |||
|---|---|---|---|---|---|---|---|---|
| Field | Total Sky | Stars | Galaxies | Stars | Intensity | Galactic | Galaxies | Galaxies |
| ID | (ST) | (SSL) | (SGL) | (ISL) | (I(Hα)) | Light (DGL) | (IGL) | (BIGL) |
| NHTF01 | 22.82 ± 0.77 | 6.19 ± 0.62 | 0.10 ± 0.01 | 1.16 ± 0.18 | 0.12 ± 0.01 | 4.54 ± 0.95 | 6.61 ± 1.24 | 1.83 ± 0.12 |
| NCOB01 | 23.15 ± 0.50 | 6.59 ± 0.66 | 0.10 ± 0.01 | 1.78 ± 0.22 | 0.17 ± 0.01 | 4.46 ± 1.04 | 6.61 ± 1.24 | 1.17 ± 0.07 |
| NCOB02 | 24.99 ± 0.54 | 6.79 ± 0.68 | 0.10 ± 0.01 | 1.63 ± 0.21 | 0.19 ± 0.01 | 5.28 ± 1.14 | 6.61 ± 1.24 | 1.63 ± 0.16 |
| NCOB03 | 22.93 ± 0.63 | 6.64 ± 0.66 | 0.10 ± 0.01 | 1.66 ± 0.21 | 0.21 ± 0.01 | 4.60 ± 1.01 | 6.61 ± 1.24 | 1.47 ± 0.06 |
| NCOB04 | 20.68 ± 0.50 | 7.32 ± 0.73 | 0.10 ± 0.01 | 1.27 ± 0.18 | 0.24 ± 0.01 | 3.30 ± 0.93 | 6.61 ± 1.24 | 1.16 ± 0.02 |
| NCOB05 | 20.82 ± 0.54 | 5.88 ± 0.59 | 0.10 ± 0.01 | 0.99 ± 0.16 | 0.10 ± 0.01 | 3.45 ± 0.94 | 6.61 ± 1.24 | 1.13 ± 0.07 |
| NCOB06 | 19.74 ± 0.64 | 5.09 ± 0.51 | 0.10 ± 0.01 | 1.09 ± 0.17 | 0.15 ± 0.01 | 4.44 ± 0.93 | 6.61 ± 1.24 | 2.06 ± 0.06 |
| NCOB07 | 20.37 ± 0.42 | 4.75 ± 0.47 | 0.10 ± 0.01 | 0.94 ± 0.16 | 0.08 ± 0.01 | 4.89 ± 0.87 | 6.61 ± 1.24 | 1.80 ± 0.14 |
| NCOB08 | 24.25 ± 0.61 | 8.10 ± 0.81 | 0.10 ± 0.01 | 2.13 ± 0.23 | 0.17 ± 0.01 | 4.40 ± 1.03 | 6.61 ± 1.24 | 1.51 ± 0.07 |
| NCOB09 | 19.92 ± 0.71 | 6.31 ± 0.63 | 0.10 ± 0.01 | 1.02 ± 0.16 | 0.13 ± 0.01 | 4.16 ± 0.93 | 6.61 ± 1.24 | 2.66 ± 0.08 |
| NCOB10 | 20.53 ± 0.58 | 6.68 ± 0.67 | 0.10 ± 0.01 | 0.93 ± 0.16 | 0.08 ± 0.01 | 3.30 ± 0.81 | 6.61 ± 1.24 | 2.78 ± 0.10 |
| NCOB11 | 19.28 ± 0.41 | 6.46 ± 0.65 | 0.10 ± 0.01 | 0.95 ± 0.16 | 0.09 ± 0.01 | 3.74 ± 1.00 | 6.61 ± 1.24 | 0.73 ± 0.06 |
| NCOB12 | 27.99 ± 0.52 | 6.02 ± 0.60 | 0.10 ± 0.01 | 1.64 ± 0.21 | 0.10 ± 0.01 | 9.72 ± 0.92 | 6.61 ± 1.24 | 1.53 ± 0.04 |
| NCOB13 | 26.74 ± 0.67 | 6.20 ± 0.62 | 0.10 ± 0.01 | 1.76 ± 0.21 | 0.11 ± 0.01 | 8.36 ± 0.99 | 6.61 ± 1.24 | 1.60 ± 0.05 |
| NCOB14 | 34.86 ± 0.58 | 9.30 ± 0.93 | 0.10 ± 0.01 | 1.83 ± 0.22 | 0.23 ± 0.01 | 13.75 ± 1.11 | 6.61 ± 1.24 | 2.51 ± 0.06 |
| NCOB15 | 26.73 ± 0.66 | 8.26 ± 0.83 | 0.10 ± 0.01 | 2.18 ± 0.24 | 0.11 ± 0.01 | 5.31 ± 1.06 | 6.61 ± 1.24 | 1.39 ± 0.03 |
| DCAL01 | 24.01 ± 0.71 | 6.81 ± 0.68 | 0.10 ± 0.01 | 1.04 ± 0.17 | 0.12 ± 0.01 | 6.96 ± 0.89 | 6.61 ± 1.24 | 2.81 ± 0.07 |
| DCAL02 | 22.88 ± 0.60 | 6.48 ± 0.65 | 0.10 ± 0.01 | 1.05 ± 0.17 | 0.23 ± 0.01 | 7.75 ± 0.91 | 6.61 ± 1.24 | 1.15 ± 0.03 |
| DCAL03 | 26.02 ± 0.84 | 8.24 ± 0.82 | 0.10 ± 0.01 | 1.91 ± 0.22 | 0.18 ± 0.01 | 8.81 ± 1.15 | 6.61 ± 1.24 | 1.82 ± 0.06 |
| DCAL04 | 29.36 ± 0.53 | 8.71 ± 0.87 | 0.10 ± 0.01 | 2.04 ± 0.23 | 0.15 ± 0.01 | 13.04 ± 1.15 | 6.61 ± 1.24 | 1.85 ± 0.48 |
| DCAL05 | 30.23 ± 0.78 | 8.06 ± 0.81 | 0.10 ± 0.01 | 1.90 ± 0.23 | 0.17 ± 0.01 | 10.61 ± 1.29 | 6.61 ± 1.24 | 2.08 ± 0.09 |
| DCAL06 | 37.86 ± 0.81 | 8.64 ± 0.86 | 0.10 ± 0.01 | 1.64 ± 0.21 | 0.21 ± 0.01 | 19.71 ± 1.16 | 6.61 ± 1.24 | 3.07 ± 0.07 |
| DCAL07 | 43.98 ± 0.75 | 6.70 ± 0.67 | 0.10 ± 0.01 | 1.81 ± 0.22 | 0.20 ± 0.01 | 24.09 ± 1.24 | 6.61 ± 1.24 | 2.49 ± 0.08 |
| DCAL08 | 45.42 ± 0.93 | 7.82 ± 0.78 | 0.10 ± 0.01 | 2.20 ± 0.24 | 0.20 ± 0.01 | 24.22 ± 1.31 | 6.61 ± 1.24 | 1.35 ± 0.06 |
Note. Values in this table are given in units of nW m−2 sr−1. The integrated intensities from faint stars (column (5)) and faint galaxies (column (8)) cover the apparent magnitude range 19.9 < V ≤ 30 mag AB. The integrated intensities from bright galaxies (column (9)) cover the range V ≤ 19.9 and are derived from DESI/DECam Legacy Survey observations. Hα intensities in this table (column (6)) are computed from the values (in rayleigh units) from Table 3 multiplied by the conversion factor 0.24 nW m−2 sr−1 R−1 at 6563 Å. The DGL values are computed using Equation (8) and the DGL errors are obtained from the Monte Carlo simulations.
Download table as: ASCIITypeset image
Table 5. Linear Fit Parameters to Relations between Single-band FIR Intensity and DGL+
| Wavelength | Slope | Intercept | Fit rms | R | CIB Monopole | CIB |
|---|---|---|---|---|---|---|
| (μm) | (nW m−2 sr−1)/(MJy sr−1) | (nW m−2 sr−1) | (nW m−2 sr−1) | Value | (MJy sr−1) | Reference |
| 100 | 10.09 ± 0.59 | 0.53 ± 0.68 | 2.82 | 0.895 | 0.780 ± 0.210 | Lagache et al. (2000) |
| 350 | 15.44 ± 0.84 | 1.71 ± 0.58 | 1.61 | 0.968 | 0.576 ± 0.034 | Odegard et al. (2019) |
| 550 | 45.85 ± 2.48 | 2.97 ± 0.53 | 1.47 | 0.973 | 0.371 ± 0.009 | Odegard et al. (2019) |
| 849 | 92.87 ± 6.22 | 7.26 ± 0.39 | 4.01 | 0.785 | 0.149 ± 0.006 | Odegard et al. (2019) |
Note. The intercept values are dependent on the CIB monopole values, which are thus listed here (see Section 4.2). The slope of the relationship between FIR intensity and DGL+ is independent of the CIB monopole value. These linear fits are provided for reference only. We do not use them in deriving the estimate of the COB in this work.
Download table as: ASCIITypeset image
One possible reason for larger scatter in the estimators at 100 μm versus 550 μm is field-to-field variation in the dust temperature. The average dust temperature for the NCOB and DCAL fields is 20.1 K, with a dispersion of 1.9 K. Variation in dust temperature can cause variations in the strength of the FIR intensity emitted for the same surface density of dust and the same optical light scattered. At 20 K, 100 μm falls on the short-wavelength side of the peak of the blackbody spectrum, and thus 100 μm emission is more sensitive to small temperature changes than is the intensity at 550 μm, which falls on the long-wavelength side of the peak. We thus investigated two-band DGL estimators, finding that using the 350 μm and 550 μm intensities in combination gives the best performance, returning smaller scatter than the 550 μm single-band estimator.
In detail, the two-band estimator fits the DGL+ value for any field as

where the subscripts on the intensities indicate that the CIB intensity has been subtracted from them. The mean 350–550 μm intensity ratio is subtracted from ratio for each field to strongly reduce covariance of the intensity-ratio term with the overall intercept term. The fit of this estimator is shown in Figure 8, with coefficient values c1 = 2.60, c2 = 48.01, and c3 = 0.96, with rms residuals of 1.39 nW m−2 sr−1. The mean 350–550 μm intensity ratio for our sample is 3.66.
Figure 8. This DGL estimator uses both Planck HFI 350 μm and 550 μm background intensities as input. The 550 μm intensity is modified by the residual of the ratio of 350 μm to 550 μm intensity about the mean value of their ratio.
Download figure:
Standard image High-resolution imageTo use the two-band estimator to predict just the DGL value, we subtract the c1 coefficient, as the predicted DGL must go to zero when the FIR intensity goes to zero. Specifically, our DGL predictor is

where the FIR intensities are in units of MJy sr−1 and the predicted DGL value is in units of nW m−2 sr−1. The estimated DGL values for all NCOB and DCAL fields are given in Table 4. The errors in Table 4 are the quadrature sums of the random and systematic errors. Those individual random and systematic errors are given in Table 6. The errors for DGL are the rms values obtained from the Monte Carlo analysis described in Section 5.
Table 6. Systematic and Random Errors for Each Intensity Component
| Scattered Light from | Faint | Hα | Diffuse | Faint | Bright | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Field | Total Sky | Stars | Galaxies | Stars | Intensity | Gal. Light | Galaxies | Galaxies | ||||||||
| ID | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) | (sys) | (ran) |
| NHTF01 | 0.16 | 0.75 | 0.62 | 0.00 | 0.01 | 0.00 | 0.17 | 0.06 | 0.00 | 0.01 | 0.94 | 0.13 | 0.97 | 0.78 | 0.11 | 0.03 |
| NCOB01 | 0.16 | 0.47 | 0.66 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 1.03 | 0.14 | 0.97 | 0.78 | 0.07 | 0.00 |
| NCOB02 | 0.16 | 0.52 | 0.68 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 1.13 | 0.15 | 0.97 | 0.78 | 0.16 | 0.01 |
| NCOB03 | 0.16 | 0.61 | 0.66 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 1.00 | 0.14 | 0.97 | 0.78 | 0.06 | 0.01 |
| NCOB04 | 0.16 | 0.47 | 0.73 | 0.00 | 0.01 | 0.00 | 0.17 | 0.06 | 0.00 | 0.01 | 0.92 | 0.13 | 0.97 | 0.78 | 0.02 | 0.01 |
| NCOB05 | 0.16 | 0.52 | 0.59 | 0.00 | 0.01 | 0.00 | 0.15 | 0.05 | 0.00 | 0.01 | 0.94 | 0.13 | 0.97 | 0.78 | 0.07 | 0.01 |
| NCOB06 | 0.16 | 0.62 | 0.51 | 0.00 | 0.01 | 0.00 | 0.16 | 0.06 | 0.00 | 0.01 | 0.92 | 0.13 | 0.97 | 0.78 | 0.06 | 0.01 |
| NCOB07 | 0.16 | 0.39 | 0.47 | 0.00 | 0.01 | 0.00 | 0.15 | 0.05 | 0.00 | 0.01 | 0.86 | 0.12 | 0.97 | 0.78 | 0.14 | 0.01 |
| NCOB08 | 0.16 | 0.59 | 0.81 | 0.00 | 0.01 | 0.00 | 0.22 | 0.08 | 0.00 | 0.01 | 1.02 | 0.14 | 0.97 | 0.78 | 0.07 | 0.01 |
| NCOB09 | 0.16 | 0.69 | 0.63 | 0.00 | 0.01 | 0.00 | 0.15 | 0.05 | 0.00 | 0.01 | 0.92 | 0.13 | 0.97 | 0.78 | 0.08 | 0.02 |
| NCOB10 | 0.16 | 0.56 | 0.67 | 0.00 | 0.01 | 0.00 | 0.15 | 0.05 | 0.00 | 0.01 | 0.80 | 0.11 | 0.97 | 0.78 | 0.10 | 0.01 |
| NCOB11 | 0.16 | 0.38 | 0.65 | 0.00 | 0.01 | 0.00 | 0.15 | 0.05 | 0.00 | 0.01 | 0.99 | 0.14 | 0.97 | 0.78 | 0.06 | 0.01 |
| NCOB12 | 0.16 | 0.49 | 0.60 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 0.91 | 0.12 | 0.97 | 0.78 | 0.04 | 0.02 |
| NCOB13 | 0.16 | 0.65 | 0.62 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 0.98 | 0.14 | 0.97 | 0.78 | 0.05 | 0.01 |
| NCOB14 | 0.16 | 0.56 | 0.93 | 0.00 | 0.01 | 0.00 | 0.21 | 0.07 | 0.00 | 0.01 | 1.10 | 0.15 | 0.97 | 0.78 | 0.06 | 0.01 |
| NCOB15 | 0.16 | 0.64 | 0.83 | 0.00 | 0.01 | 0.00 | 0.23 | 0.08 | 0.00 | 0.01 | 1.05 | 0.14 | 0.97 | 0.78 | 0.03 | 0.02 |
| DCAL01 | 0.16 | 0.69 | 0.68 | 0.00 | 0.01 | 0.00 | 0.16 | 0.06 | 0.00 | 0.01 | 0.88 | 0.12 | 0.97 | 0.78 | 0.07 | 0.01 |
| DCAL02 | 0.16 | 0.58 | 0.65 | 0.00 | 0.01 | 0.00 | 0.16 | 0.06 | 0.00 | 0.01 | 0.90 | 0.12 | 0.97 | 0.78 | 0.03 | 0.01 |
| DCAL03 | 0.16 | 0.82 | 0.82 | 0.00 | 0.01 | 0.00 | 0.21 | 0.07 | 0.00 | 0.01 | 1.14 | 0.16 | 0.97 | 0.78 | 0.05 | 0.03 |
| DCAL04 | 0.16 | 0.51 | 0.87 | 0.00 | 0.01 | 0.00 | 0.22 | 0.08 | 0.00 | 0.01 | 1.14 | 0.16 | 0.97 | 0.78 | 0.48 | 0.02 |
| DCAL05 | 0.16 | 0.76 | 0.81 | 0.00 | 0.01 | 0.00 | 0.21 | 0.07 | 0.00 | 0.01 | 1.28 | 0.18 | 0.97 | 0.78 | 0.09 | 0.02 |
| DCAL06 | 0.16 | 0.79 | 0.86 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 1.15 | 0.16 | 0.97 | 0.78 | 0.07 | 0.02 |
| DCAL07 | 0.16 | 0.73 | 0.67 | 0.00 | 0.01 | 0.00 | 0.20 | 0.07 | 0.00 | 0.01 | 1.22 | 0.17 | 0.97 | 0.78 | 0.07 | 0.02 |
| DCAL08 | 0.16 | 0.92 | 0.78 | 0.00 | 0.01 | 0.00 | 0.22 | 0.08 | 0.00 | 0.01 | 1.29 | 0.18 | 0.97 | 0.78 | 0.06 | 0.02 |
Note. Error values in this table are given in units of nW m−2 sr−1. The contribution of each error to the final COB and SU measurements are determined using a Monte Carlo code that properly accounts for the random and systematic errors in every parameter. The ran/sys DGL errors are obtained directly from the Monte Carlo simulations.
Download table as: ASCIITypeset image
To visualize the relative importance of all sky components we represent the results as a stacked bar chart for each field in Figure 9. While the summed intensity from every field is less than the total sky level, the dominance of systematic errors in most of the intensity components means the uncertainty in the combined data set will not be diminished by the  factor. We present our approach for determining the proper propagation of errors for the combined suite of data in the next section.
factor. We present our approach for determining the proper propagation of errors for the combined suite of data in the next section.
Figure 9. A stacked bar chart showing the amplitudes of the known sky components for the 16 COB fields. The black horizontal lines with error bars show the measured total sky values for each field, sorted in order of increasing total sky level. The gap between the tops of the bars and the total sky measurements represents the anomalous sky intensity in each field. Note that seven fields have total skies of only ∼20 nW m−2 sr−1. The intensity of bright galaxies in the fields does not contribute to the total skies as measured, but is included in the final COB intensity. The purple points are the sum of the known intensity components represented by the stacked bars. The associated errors are provided to show the approximate significance of the gap between the sum of all known components and the total measured sky intensity. The significance of the final COB value is computed using a comprehensive Monte Carlo analysis.
Download figure:
Standard image High-resolution image5. The Cosmic Optical Background
5.1. A Monte Carlo Approach to Estimating the COB Intensity
Having identified all the sources of foreground optical emission known to us in the two previous sections, the task is then to recover an optimal estimate of the COB intensity with accurate errors that reflect the appropriate random and systematic uncertainties (see Table 6), as well as any covariances among the parameters used to estimate the COB intensity. We will use a Monte Carlo approach that randomly generates complete realizations of the COB observations as based on our error model. As noted at the start of Section 3, we do this in two steps. With the exception of the DGL component, our knowledge of all other foregrounds, as well as the total sky level itself, comes from mutually independent information. As such, we start with Equation (3) to estimate DGL+, the DGL intensity plus any anomalous intensity component, which is not affected by covariance among the terms that are subtracted off to isolate it. The second step is to then use the FIR background intensity to isolate the DGL component itself. As this uses the observations to develop a self-calibrated DGL estimator, this step does account for covariance between the observational parameters.
For the first step then, the Monte Carlo routine generates 10,000 realizations of the observations of total sky intensity and the non-DGL foreground components (ST, IGL, SSL, SGL, ISL, BIGL, and I(H α)) for each field. We also generate random realizations of the independent variables (FIR intensities and cosmic IR backgrounds) that will be used to estimate the DGL. In detail, for any observed component or observational input, Dobs(j), in field j (1 ≤ j ≤ 24; 16 NCOB + 8 DCAL fields), the Monte Carlo routine generates a set of simulated values for 1 ≤ i ≤ 104:

where GD(i, j) and FD(i) are sequences of Gaussian random variables with zero mean and unit variance. Note that FD(i) scales the systematic error term σSYS(j) in any field, and is thus the same for all fields for a given realization i. For many parameters, σSYS will also be constant over all fields, but relative systematic errors may vary from field to field in step with the given parameter (as occurs in the case of SSL, for example). In contrast, GD(i, j) scales the random errors, which vary freely from field to field in any given realization. Lastly, we note that while Equation (9) is fully general in allowing for both systematic and random errors for any component, in practice the systematic errors strongly dominate the total error budget, and for many components the random error term is negligible.
5.2. Estimating the DGL Intensities
A two-band DGL estimator of the form given by Equation (7) is generated for every Monte Carlo realization from its set of 24 DGL+ values produced, which is used to predict the DGL backgrounds for that particular realization. As is described by Equation (6), the independent variables used by the estimator are the FIR background intensities at 350 μm and 550 μ m, with the estimated CIB backgrounds subtracted. Fitting the DGL+ values to the FIR background intensities generates the c1, c2, and c3 coefficients in Equation (7). The best-fit DGL-alone estimates for each field are then provided by the c2 and c3 coefficients on the assumption that DGL is zero for zero FIR background intensity. This directly highlights the strong covariance between the assumed CIB backgrounds and the DGL predictions noted in Section 4.2. This covariance is included in the Monte Carlo routine, however, simply by including errors in all the FIR parameters as part of the analysis. The coefficients of the DGL estimator are also covariant, but again by having the Monte Carlo routine sample the error distributions of both the independent and dependent variables used by the DGL estimator, this behavior is included implicitly in the analysis as well. Further, because the DGL+ intensities for any field reflect the errors of all components used to generate them, the Monte Carlo analysis also incorporates the full suite of covariances associated with deriving the DGL estimator from the COB observations themselves.
Lastly, we note that while we presented a mean two-band DGL estimator in Equation (8), we actually do not use it as such for the final analysis. Again, we generate the DGL estimator anew for each Monte Carlo realization. Our interest is really just in the distribution of DGL estimates for any given field generated by the full ensemble of Monte Carlo runs. These distributions, in fact, rather than any simple error calculation, provide the appropriate uncertainties in the DGL values needed to derive the errors in the final COB and SU intensities.
5.3. Estimating the COB Intensity and Anomalous Background Component
With the DGL component derived for all fields in all 10,000 Monte Carlo runs, it is simple to derive the COB intensity and any residual anomalous intensity background, SU, for each realization. The optimal estimate of both parameters for the whole survey will be derived by first generating the COB and SU intensity distributions for each field, then combining them into a full ensemble distribution weighted by the inverse variance of the individual-field distributions.
The anomalous component, SU, is just the residual intensity remaining after all known sources of light are subtracted from the data. Specifically,

We compute SU for each field using the 10,000 realizations of each parameter on the right-hand side of Equation (10). We then generate the cumulative distribution function of SU for each field and find its 68.3% confidence limits. We adopt the 1σ value on SU to be half the difference between high and low 68.3% confidence limits for that specific field. We then generate a summed distribution of all the SU values for all fields, weighting the SU values for each field by the inverse square of that field's corresponding 1σ value. The value of SU for the full sample is then taken to be the mean value of that weighted sum distribution, and the error in the full sample SU is taken as the half width of the 68.3% confidence limit range of that weighted sum distribution. The resulting summed distribution of SU values for all 16 COB survey fields is shown in Figure 10.
Figure 10. The distributions of sky residuals (anomalous intensity) for each of the 16 NCOB fields, produced from 10,000 Monte Carlo realizations of each data set, are shown as colored curves. The weighted summed distribution for all 16 fields combined is shown by the black histogram. The sky residual is the intensity left over after all known sources of light are subtracted from the measured total sky level. If all known sources of light had been accounted for, then the peak of the summed distribution would be centered on zero. The actual distribution is shifted from zero but only by +1.47σ.
Download figure:
Standard image High-resolution imageTo get the optimal full-survey COB intensity, we repeat the above procedure but apply it to the following expression:

We remind the reader that we need to add back the integrated light of bright galaxies (BIGL) prior to computing the COB since all galaxies brighter than V = 19.9 had been masked out prior to measuring the total sky level (see Section 3.1 for details). The resulting summed distribution of COB values for all 16 survey fields is shown in Figure 11.
Figure 11. The distributions of cosmic optical background values for each of the 16 NCOB fields, produced from 10,000 Monte Carlo realizations of each data set, are shown as colored curves. The weighted summed distribution for all 16 fields combined is shown by the black histogram. The predicted extragalactic background intensity in the optical passband from a variety of galaxy surveys is shown by the vertical gray bar. The width of the gray bar is set by the uncertainty in the integrated light from known galaxies. The mean of the measured COB distribution from this work differs from zero by +6.77σ, representing one of the most significant detections of the COB to date.
Download figure:
Standard image High-resolution imageOur derived COB and SU values are

The COB is detected at a significance of 6.77σ but the anomalous (residual) sky intensity is only present at the 1.47σ level. In other words, SU is likely consistent with zero.
5.4. Jackknife Tests of the Robustness of the Results
To determine whether any one of our NCOB or DCAL fields has an outsized influence on either the COB or SU estimate, we perform a series of jackknife tests, where for each test we exclude just one field from the Monte Carlo simulations, doing this in turn for each field in the full set of 16 NCOB and 8 DCAL fields. The outcomes of these tests are shown in Figure 12. The x-axis labels show the name of the field that was excluded in each 10,000 run simulation. The red and blue data points show, respectively, the resulting COB and SU values derived when that field was excluded from the analysis. The standard deviation in the COB or SU for these 24 jackknife tests is just 0.12 nW m−2 sr−1. We conclude that the COB and SU results are resilient against the removal of any one of the NCOB or DCAL fields from the analysis.
Figure 12. Jackknife test results are shown for the COB and SU intensity measurements. The data points show the intensities calculated when the indicated NCOB or DCAL field (shown along the x-axis) is excluded from the analysis. The central y-values and heights of the red and blue horizontal bands are the derived values and their 1σ ranges for the full-sample COB and SU, respectively. No field is seen to have an outsized influence on the results using the total sample.
Download figure:
Standard image High-resolution image5.5. Results for the Interplanetary Dust Field
As noted in Section 2.1, we obtained observations of four fields at low ecliptic latitude to verify the assumption that there is no significant ZL emission at heliocentric distances beyond 50 au. We perform this test by computing the COB and SU intensity values for the four IPD fields and look for any significant deviations from the main survey results listed in Equation (12). The results are given in Table 7. Because the IPDF observations were not part of our rigorous survey selection process, the errors on the COB and SU values for the IPD fields are estimated analytically rather than with the Monte Carlo procedure but should be approximately similar to what the Monte Carlo process would yield. Columns (3) and (5) in Table 7 give the difference between the COB and SU given in Equation (12) and the corresponding values for each IPD field, respectively. We find no significant differences between the COB and SU values obtained for the IPD fields and those derived from the COB science fields, supporting the assertion that ZL is negligible at the distances where NH made the COB observations presented here. The consistency between the COB science observations and the IPDF observations also suggests that there are no major zodiacal subtraction residuals in the Planck HFI maps.
Table 7. COB and SU Results for the IPD Fields
| Field | COB | ΔCOB | SU | ΔSU |
|---|---|---|---|---|
| ID | Value | (NCOB – IPDF) | Value | (NCOB – IPDF) |
| IPDF01 | 8.78 ± 2.59 | − 2.38 ± 3.07 | 0.61 ± 2.88 | − 2.38 ± 3.52 |
| IPDF02 | 11.24 ± 2.79 | −0.08 ± 3.24 | 3.18 ± 3.05 | −0.19 ± 3.66 |
| IPDF03 | 12.10 ± 2.14 | −0.94 ± 2.70 | 2.69 ± 2.47 | − 0.30 ± 3.20 |
| IPDF04 | 11.15 ± 2.02 | − 0.01 ± 2.61 | 3.44 ± 2.36 | −0.45 ± 3.11 |
Note. All values are in units of nW m−2 sr−1.
Download table as: ASCIITypeset image
5.6. Isotropy of the COB
With 16 fields spread over the sky, we can, in principle, look for anisotropy in the COB. Of the 16 NCOB fields, 13 are in the south Galactic hemisphere (SGH) and three are in the north Galactic hemisphere (NGH). We derive the COB for these two subsets to see whether there are any significant offsets between them. We use the 10,000 realizations generated and separate out the north and south Galactic subsamples from them. The COB and SU values are then calculated. The results are shown in Table 8. We also plot the individual SU values as a function of ecliptic and Galactic latitude in Figure 13. We do not see any significant difference between the COB or SU values derived for the NGH versus SGH subsamples. Nor do we seen any significant trend with ecliptic latitude with the current sample. We note that with only three NCOB fields in the NGH and only three DCAL fields in the SGH, we use the full sample to compute the two-band DGL estimator in this isotropy analysis. A larger NGH NCOB sample and more DCAL observations in the SGH would be required to do a more in-depth exploration of any anisotropy in the COB signal.
Figure 13. The sky residual signal, SU, as a function of Galactic latitude (top) and ecliptic latitude (bottom) for each individual NCOB field. The yellow horizontal band shows the sky residual ±1σ range for the full sample of 16 fields. No significant trend is seen between SU and ecliptic or Galactic latitude.
Download figure:
Standard image High-resolution imageTable 8. COB and SU Results for the North and South Galactic Hemispheres
| Galactic | COB | Stat. | SU | Stat. | Number of |
|---|---|---|---|---|---|
| Hemisphere | Value | Signif. | Value | Signif. | Fields |
| North | 11.91 ± 1.34 | 8.92 | 4.16 ± 1.96 | 2.12 | 3 |
| South | 10.93 ± 1.64 | 6.65 | 2.80 ± 2.00 | 1.40 | 13 |
Note. COB and SU values are in units of nW m−2 sr−1.
Download table as: ASCIITypeset image
6. Convergence
Broadly speaking, there are three ways to measure the intensity of the COB. In one approach, determining the COB intensity is a natural outcome of a panoramic and lengthy campaign to identify and assay all light sources in the Universe. In practice, this means beginning with a complete census of galaxies and their associated active nuclei. Galaxies exist, therefore there must be a COB. The tally of known light-emitting objects always defines the lower limit to the COB intensity. A second approach is inferential. The existence of the COB implies that very-high-energy (VHE) γ-rays cannot freely traverse the Universe. Their observed extinction as a function of cosmological distance to their source active galactic nuclei provides an estimate of the COB intensity. The third and final approach is that attempted here: direct observation of the COB intensity. This requires care to isolate and correct for irrelevant foreground intensity sources, but also allows for the discovery of previously unknown intensity sources.
At the outset of this work we posed the question: Is the COB intensity as expected from our census of faint galaxies, or does the Universe contain additional sources of light not yet recognized? With our present result, it appears that these diverse approaches are converging to a common answer. Galaxies are the greatly dominant and perhaps even complete source of the COB. There does remain some room for interesting qualifications and adjustments to this picture, but in broad outline it is the simplest explanation for what we see.
Figure 14 shows our present result in the context of COB measurements from all three methods. We presented a previous version of this figure in NH22, but we revisit it here in light of our revised estimate of the COB intensity and the greatly reduced allowance for an anomalous COB component. As we noted in NH22, there is excellent agreement on the IGL level over the ensemble of estimates. Driver et al. (2016), Saldana-Lopez et al. (2021), and our own estimate (see NH21) all imply a contribution to the COB intensity of ∼8 nW m−2 sr−1 over the passband sampled by LORRI. At the same time, the galaxy counts feeding into the IGL are obtained from similar, if not the same, observational sources, and thus may have common systematic errors. For example, Conselice et al. (2016) argued that the galaxy counts are seriously incomplete, while Cooray et al. (2012), Zemcov et al. (2014), and Matsumoto & Tsumura (2019) argued that the COB includes a substantial component of light from stars tidally removed from galaxies, or from a population of faint sources in extended halos. Our present COB intensity would indeed allow for a modest enhancement in the implied starlight contribution to the COB, but not a wholesale revision of it. To explain the SU value of 2.91 ± 2.03 nW m−2 sr−1 as extragalactic in origin would require a ∼37(±7)% increase in light from galaxies or intergalactic space, corresponding to the ratio of our COB value (11.16 nW m−2 sr−1) to that predicted from deep galaxy counts (= IGL + BIGL = 8.17 nW m−2 sr−1). Driver et al. (2016) suggest a diffuse component to extragalactic background light could be present at the 20% level, possibly due to low-surface-brightness galaxies and/or intrahalo light in the specific case of the COB spectrum accessible to LORRI. We note that if we extend the integration limit on galaxy counts at the faint end to V = 34 mag instead of V = 30 mag and we assume that the faint-end slope of the relation between galaxy number counts and magnitude remains unchanged, our IGL estimate would increase by ∼8% with a corresponding reduction in SU.
Figure 14. The present result is compared to previous COB measurements over the wavelengths spanned by the LORRI passband. Direct COB intensity measurements are shown as points with error bars. The NH21 and NH22 intensities are slightly offset to the blue for clarity. The Zemcov et al. (2017) intensity limit (offset to the red for clarity) and the Mattila et al. (2017) 0.52 μm limit are shown as 2σ upper limits. The NH22 intensity is shown twice. The upper point is the intensity as published in NH22. The lower point is the NH22 intensity revised to correct the DGL subtraction error noted in Section 4. IGL estimates are shown as lines with 1σ bounds. COB intensities inferred from VHE γ-rays are shown as shaded bands.
Download figure:
Standard image High-resolution imageWe show the COB constraints from five recent VHE (0.1−30 TeV) γ-ray studies: Ahnen et al. (2016), H.E.S.S. Collaboration et al. (2017), Fermi-LAT Collaboration et al. (2018), Desai et al. (2019), and Acciari et al. (2019) in Figure 14. The concordance of the COB inferred from galaxy counts and VHE γ-ray absorption has already long been advanced as a strong argument that the COB is mainly due to the light of known galaxies. A significantly higher COB intensity would engender significantly higher VHE γ-ray extinction. One interesting caveat, however, is that most of these studies assume that the spectral energy distribution of the COB photons is the same as that of the IGL. When the analysis allows for arbitrary intensity as a function of wavelength, as was done in the H.E.S.S. Collaboration et al. (2017) and Acciari et al. (2019) papers (shown in Figure 14 with light shading), the VHE γ-ray constraints can allow for considerably larger COB intensity than that associated with the IGL alone.
Figure 14 shows several examples of direct-detection COB measurements largely made from near-Earth space that fall within the LORRI passband. As was discussed in NH22, these include the HST/WFPC2 observations of Bernstein (2007), the Pioneer measurements of Matsuoka et al. (2011), the CIBER rocket-based measurements of Matsuura et al. (2017), and the "dark cloud" measurements of Mattila et al. (2017). The 0.40 μm intensity of Mattila et al. (2017) and the 0.80 μm CIBER intensity of Matsuura et al. (2017) reject a null detection of the COB with only slightly better than 2σ significance. Most of the measurements are not significantly different than zero. More recently, the SKYSURF project (Carleton et al. 2022) attempted to detect the COB in three near-infrared bands to the red of 1 μm, using archival HST observations, but only achieved upper limits of 29 nW m−2 sr−1. It is still extremely difficult to get past the strong effects of ZL in the inner solar system.
Our present COB measurement of 11.16 ± 1.65 nW m−2 sr−1 is plotted in Figure 14 with the "NH" label. The most important contrast with our earlier work is the present 32% downward revision of the COB intensity as compared to the 16.37 ± 1.47 nW m−2 sr−1 intensity in NH22, based on NHTF01. As noted in Section 4, we concluded that the DGL contribution to NHTF01 had been seriously underestimated due to an incorrect correction that we applied to the foreground 100 μm intensity that we used with the Zemcov et al. (2017) DGL estimator. In Figure 14 we also plot the NH22 result with the revised 100 μm intensity as "NH22 Rev" to demonstrate the effect of this revision alone. The error bars increase with the larger implied DGL correction, but this intensity is now in excellent agreement with the present COB intensity. Again, the NHTF01 image set is fully included in our present analysis with all the revisions noted in Table 1, including the new DGL estimator developed in Section 4 and the count-rate decay correction presented in Section 2.5.
We note that our present COB intensity is only ∼50% of the 21.98 ± 1.83 (1.23 stat, 1.36 sys) nW m−2 sr−1 COB intensity reported by Symons et al. (2023). As that measurement is made with LORRI as well, and indeed incorporates all the archival data presented in NH21 (albeit with additional archival data that we chose not to use in NH21), this is concerning. At present we cannot resolve this difference. We can only remark that the Symons et al. (2023) analysis was independent of ours and made several choices concerning the archival data used and the detailed processing that differ from ours. We also note that the raw total sky intensities for seven of our 16 fields before any foreground intensity sources were subtracted are already less than the final Symons et al. (2023) COB intensity (see Figure 9 or Table 4).
If our present COB intensity is correct, however, it means that galaxy counts, VHE γ-ray extinction, and direct optical band measurements of the COB intensity have finally converged at an interesting level of precision. There is still room to adjust the galaxy counts slightly, or to allow for nondominant anomalous intensity sources. But the simplest hypothesis appears to provide the best explanation of what we see: the COB is the light from all the galaxies within our horizon.
Acknowledgments
We thank NASA for funding and continued support of the New Horizons mission, which were required to obtain the present observations. No New Horizons NASA funds were used, however, for the reduction and analysis of the 2023 NH COB observations. The data presented were obtained during the second Kuiper Extended Mission of New Horizons. We thank Bruce Draine and Jean-Marc Casandjian for useful conversations. We thank the anonymous referee for the careful review and insightful comments that helped us to improve the clarity of this paper. M.P. is funded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc. (AURA), under NASA contract NAS 526555. T.R.L. is funded by NSF NOIRLab, which is managed by AURA under a cooperative agreement with the National Science Foundation. We also thank the Aspen Center for Physics for their hospitality during our time completing this paper. The Aspen Center for Physics is supported by National Science Foundation grant PHY-2210452.
This work made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work also made use of data obtained with Planck (https://www.esa.int/Science_Exploration/Space_Science/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada.
This research uses services or data provided by the Astro Data Lab, which is part of the Community Science and Data Center (CSDC) program at NSF's National Optical–Infrared Astronomy Research Laboratory. NOIRLab is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under a cooperative agreement with the National Science Foundation. This research has also made use of the NASA/IPAC Infrared Science Archive, which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology.
Software: astropy (Astropy Collaboration et al. 2013, 2018), matplotlib (Hunter 2007), TRILEGAL (Girardi et al. 2005), Vista (Lauer et al. 1983).
Footnotes
- 13
- 14
As a consequence of this small tweaking of field position, one field—NCOB12—falls slightly below the ∣β∣ = 15° limit.

















