Abstract
The 30 yr orbit of the Cepheid Polaris has been followed with observations by the Center for High Angular Resolution Astronomy (CHARA) Array from 2016 through 2021. An additional measurement has been made with speckle interferometry at the Apache Point Observatory. Detection of the companion is complicated by its comparative faintness—an extreme flux ratio. Angular diameter measurements appear to show some variation with pulsation phase. Astrometric positions of the companion were measured with a custom grid-based model-fitting procedure and confirmed with the CANDID software. These positions were combined with the extensive radial velocities (RVs) discussed by Torres to fit an orbit. Because of the imbalance of the sizes of the astrometry and RV data sets, several methods of weighting are discussed. The resulting mass of the Cepheid is 5.13 ± 0.28 M⊙. Because of the comparatively large eccentricity of the orbit (0.63), the mass derived is sensitive to the value found for the eccentricity. The mass combined with the distance shows that the Cepheid is more luminous than predicted for this mass from evolutionary tracks. The identification of surface spots is discussed. This would give credence to the identification of a radial velocity variation with a period of approximately 120 days as a rotation period. Polaris has some unusual properties (rapid period change, a phase jump, variable amplitude, and unusual polarization). However, a pulsation scenario involving pulsation mode, orbital periastron passage, and low pulsation amplitude can explain these characteristics within the framework of pulsation seen in Cepheids.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The importance of Cepheid variable stars as the first step in the cosmological distance scale has been emphasized recently in the discussion of the tension between the Hubble constant H0 from Cepheids and Type Ia supernovae and that from the early Universe based on Planck cosmic microwave background observations (Riess et al. 2021).
Another property of Cepheids, their masses, provides pivotal tests of stellar evolution and predictions of the production of end-stage objects such as neutron stars. In stellar evolution calculations, the luminosity at the Cepheid stage depends on main-sequence core convective overshooting and rotation in Cepheid progenitors (B stars; Anderson et al. 2014) and also mass loss (see, e.g., Neilson et al. 2012). Asteroseismology from space-based observations is revolutionizing stellar evolution calculations by providing information about the internal structure of stars (Kurtz 2022). Comparing the mass–luminosity (ML) relation from calculations with observed quantities is an important test. The persistent "Cepheid mass problem" (the disagreement between masses inferred from evolutionary tracks and from pulsation calculations) has been reduced to about 10% (Bono et al. 2001; Neilson et al. 2011) but still remains. While calibration of Cepheid luminosities will be significantly improved in the final Gaia release, their masses can only be measured directly in binary systems, and hence only a limited number are available, one of which is Polaris.
A further motivation for determining the masses of Milky Way (MW) Cepheids as accurately as possible is that six Cepheids have been found to be members of eclipsing binaries in the Large Magellanic Cloud (LMC; Pilecki et al. 2018, 2021), so comparison between the ML relations for the metallicities of the MW and the LMC can now be made.
Cepheids have typical masses of about 4–5 M⊙, but the longest-period Cepheids may be as massive as ∼11 M⊙ (Anderson et al. 2014). Most Cepheids are fated to become white dwarfs; however, the most massive may become supernovae, and end their lives as neutron stars. As an example of the importance of the calibration of the Cepheid ML relation, V1334 Cyg is the Cepheid in the MW that has the most accurate dynamical mass (accurate to 3%; Gallenne et al. 2018). This mass is smaller than predicted by evolutionary tracks. This means that the fraction of Cepheids that are massive enough to become neutron stars could be smaller than expected, leading to implications for the frequency of neutron stars.
Mass determination starts with a radial velocity (RV) orbit and pulsation curve for a binary containing a Cepheid. At the present time several new capabilities are available which make it possible to directly measure model-independent, dynamical masses for Cepheids using this orbit. Interferometry has resolved a number of systems, providing the semimajor axis, a = a1 + a2, and the inclination, i. The Center for High Angular Resolution Astronomy (CHARA) Array and the Very Large Telescope Interferometer make it possible to reach stars in both hemispheres. In addition, high-resolution spectra in the ultraviolet (UV) from Hubble Space Telescope (HST) allow the orbital RV amplitude of hot companions of Cepheids to be measured. The Gaia spacecraft can provide both distances and proper motions. Astrometry is modeled by a sum of constant proper motion and an astrometric orbit, including the inclination. Final versions of proper motions and distances will not be available for Cepheids generally until the Gaia DR4 data release that includes orbital solutions in the astrometry routinely.
The accuracy of inputs from any of these measurements depends on many characteristics of the star: brightness, orbital period, inclination, and separation, distance, and mass ratio of the components. This means that each Cepheid system is unique and has to be analyzed independently. The system under discussion here (Polaris), for instance, has a comparatively low mass companion. It is not possible to measure a velocity of the companion with HST UV spectra. It is also too bright to be accurately measured by Gaia, so the distance determination depends on a third star in the system, as discussed below. However, because it is the nearest Cepheid, and has a long-period orbit, the system has been resolved by HST, CHARA, and speckle interferometry at Apache Point Observatory (APO). The long orbital period, however, results in a low velocity amplitude and the need to make use of a combination of RVs from many instruments. Both the low orbital velocity amplitude and the use of data from many sources are challenges for the basic orbit determination, which have recently been addressed in the spectroscopic study of Torres (2023).
This study is part of a series to incorporate current capabilities into studies of Cepheid masses.
1.1. Polaris
Polaris (α UMi, HR 424, HD 8890, V = 2.02 mag) is the nearest and brightest classical Cepheid. It is a member of a triple system with a resolved eighth magnitude physical companion at a separation of 18''. The Cepheid has been known for many years to be a single-lined spectroscopic binary with a period of about 30 yr (Roemer 1965; Kamper 1996), with components designated Aa (the Cepheid) and Ab. A thorough compilation of RV data has recently been produced by Torres (2023), resulting in a definitive orbit.
While Polaris Aa is a Cepheid, albeit with a small amplitude, it has several characteristics that are unusual.
- 1.It pulsates in the first overtone (Feast & Catchpole 1997).
- 2.
- 3.The pulsation amplitude can vary. Specifically, it decreased from about 1960 to 1990 (Arellano Ferro 1983). However, it did not die out completely (cease pulsation), but in about 2000 began to increase (e.g., Bruntt et al. 2008; Anderson 2019). Anderson, indeed, found the amplitude to be very stable over the course of 7 yr.
- 4.
- 5.
- 6.
- 7.The single observation of Polaris to detect polarization (Barron et al. 2022) found a much more complicated Stokes V profile than for other Cepheids implying a complex magnetic field. However, the profile is similar to the nonvariable supergiant α Per (Grunhut et al. 2010), which perhaps reflects the very low pulsation amplitude.
- 8.Several studies have searched for additional periodicities in the RVs (Lee et al. 2008; Anderson 2019, and other studies discussed therein). A periodicity of approximately 120 days was found by Lee et al., for instance, which they identify as due to rotation in a star with spots. Two periodicities (40.2 and 60 days) were found by Anderson; 120 days is an integral multiple of these.
These topics are fully discussed and references to all the velocity data sources are provided by Torres (2023). In this discussion these apparently exceptional properties are placed in the context of Cepheids. The times of periastron passage of Polaris coincide with the amplitude changes and also the phase jump at about 1960. In the extensive study of period changes in Cepheids, Csornyei et al. (2022) find a number with phase jumps, as was found by Szabados previously (Szabados 1991, 1989, and references therein). They are often found in short-period overtone pulsators, and it was suggested by Szabados (1992) that they are likely to be found in binaries. This would link a number of the peculiarities related to Polaris to phenomena seen in other Cepheids, and provide a physical explanation. On one hand, this is surprising because the Polaris Aa and Ab system is comparatively wide. Torres estimates that the periastron separation between the two stars is 6.2 au, or approximately 29 times the Cepheid radius. On the other hand, the orbit is eccentric (e = 0.635), providing a variation of conditions around the orbit. The wide orbit would make it surprising for a characteristic such as a phase jump to be produced by simple tidal interaction. However, overtone pulsators are more erratic in their periods than fundamental mode pulsators, presumably for reasons we do not completely understand. Of course, these peculiarities may exist in other stars but have not been identified because they do not have such long and well-covered data sets.
An important parameter in determining properties of Polaris is its distance. Specifically, the determination of the total mass in the system depends on the distance to convert the angular separation to au. The distance has been controversial, partly because of difficulties because Polaris is very bright. Recent distance determinations are summarized by Engle et al. (2018). Polaris B is the wide companion at a distance of 18'' from the Polaris A system. It can be used for distance determination. Bond et al. (2018) argued that Polaris A and B form a gravitationally bound system, which allows us to use Polaris B for distance determination. The distance to Polaris B using Gaia DR3 (Gaia Collaboration et al. 2023) including the Lindegren parallax offset is 136.90 ± 0.34 pc (Lindegren et al. 2021; Gaia Collaboration et al. 2023). The distance will be reviewed when the Gaia DR4 is available, including corrections such as discussed in Khan et al. (2023).
Several previous steps have led up to the measurement of the mass of the Cepheid. The binary system discussed here is Polaris A made up of the Cepheid Polaris Aa and the companion Polaris Ab. Kamper (1996) published an orbit (with additional velocities by Kamper & Fernie 1998). In addition, Wielen et al. (2000) determined the inclination and the position angle of the line of nodes by comparing the proper motion from the Hipparcos satellite with the average long-term ground-based proper motion. The final parameter to determine the mass was the separation of Aa and Ab. This system was resolved with HST (Evans et al. 2008) using the Advanced Camera for Surveys (ACS). This provided the mass of the Cepheid of  . This was followed up with three observations between 2007 and 2014 using WFPC2 and WFC3 since the ACS high-resolution channel (HRC) was no longer available (Evans et al. 2018). The astrometry from these observations was less accurate. However, since they cover a quarter of the orbit, the inclination could be determined from them as well as the separation between the components. The present paper discusses observations around the orbit continued with CHARA and a speckle observation from APO.
. This was followed up with three observations between 2007 and 2014 using WFPC2 and WFC3 since the ACS high-resolution channel (HRC) was no longer available (Evans et al. 2018). The astrometry from these observations was less accurate. However, since they cover a quarter of the orbit, the inclination could be determined from them as well as the separation between the components. The present paper discusses observations around the orbit continued with CHARA and a speckle observation from APO.
The sections below contain the CHARA interferometric observations including data reduction and analysis, the diameter and surface imaging of Polaris, APO speckle observations, the orbit fitting, and discussion of the results.
2. Interferometric Observations and Data Reduction
We collected long-baseline optical interferometric data at Georgia State University's CHARA Array (ten Brummelaar et al. 2005) located at Mount Wilson Observatory. The CHARA Array consists of six 1 m aperture telescopes in a Y-shaped configuration with two telescopes along each arm, oriented to the east (E1, E2), west (W1, W2), and south (S1, S2), offering good coverage of the (u, v) plane. The baselines range from 34 to 331 m, providing an angular resolution down to 0.5 mas at λ = 1.6 μm. The data on Polaris were collected with the Michigan InfraRed Combiner (MIRC; Monnier et al. 2004) before 2017.5 and the upgraded Michigan InfraRed Combiner-eXeter (MIRC-X; Anugu et al. 2020) after 2017.5. MIRC and MIRC-X combine the light from all six telescopes simultaneously in the H band, providing up to 15 fringe visibilities and 20 closure phase measurements across multiple spectral channels.
At the location of Polaris in the sky, we can combine only four telescopes at a time because of limitations on the length of the CHARA delay lines. Initially we used the low spectral resolution mode (prism R = λ/Δλ = 50) with MIRC and MIRC-X. Bandwidth smearing limits the effective field of view to ∼50 mas (given by λ2/Δλ) for the low spectral resolution mode. This resolution was sufficient to resolve the Ab companion during closest approach; however, detecting the companion became more challenging as the relative separation increased from orbital motion. In 2019 September, we switched to higher spectral resolution modes (prism R = 102, grism R = 190) to extend the interferometric field of view to 100 mas and 190 mas, respectively. A log of our observations is available in Table 1.
Table 1. Log of the MIRC and MIRC-X Observations at the CHARA Array
| UT Date | Combiner | Configuration | Mode | Nsets | Nspec | Nvis | NCP | Calibrators |
|---|---|---|---|---|---|---|---|---|
| 2016 Sep 12 a | MIRC | W1E1E2W2 | R = 50 | 1 | 8 | 1472 | 976 | 1, 2 |
| 2016 Nov 18 | MIRC | W1E1E2W2 | R = 50 | 1 | 8 | 1488 | 960 | 1, 2 |
| 2018 Aug 27 | MIRC-X | W1E1E2W2 | R = 50 | 3 | 10 | 5560 | 3660 | 1, 3 |
| W1S2E1E2 | R = 50 | 3 | 10 | 5740 | 3780 | 1, 3 | ||
| 2019 Apr 09 | MIRC-X | E1W2W1E2 | R = 50 | 4 | 6 | 3216 | 2016 | 1, 3 |
| E1W1S2E2 | R = 50 | 3 | 6 | 2310 | 1212 | 1, 3 | ||
| 2019 Sep 2 a | MIRC-X | E1W2W1E2 | R = 102 | 1 | 13 | 1287 | 816 | 1, 2 |
| E1W2W1E2 | R = 190 | 2 | 31 | 6076 | 3870 | 1, 2 | ||
| 2021 Apr 2 a | MIRC-X | E1W2W1E2 | R = 190 | 3 | 32 | 8256 | 5115 | 1, 3, 4 |
| E1W1S2E2 | R = 190 | 2 | 32 | 9664 | 6169 | 1, 3, 4 | ||
| 2021 Apr 3 a | MIRC-X | E1W2W1E2 | R = 190 | 5 | 33 | 11187 | 5920 | 1, 3, 4 |
| 2021 Apr 4a | MIRC-X | E1W2W1E2 | R = 190 | 4 | 33 | 9174 | 4576 | 1, 3, 4 |
| E1W1S2E2 | R = 190 | 4 | 33 | 11649 | 7520 | 1, 3, 4 |
Note. The nights of 2018–2021 include two different telescope configurations and/or different spectral modes. The table gives the number of observing sets (Nsets) and the number of spectral channels (Nspec). It also lists the number of visibility (Nvis) and closure phase (NCP) measurements for the reduction using the 30 s integration time. We adopted uniform disk diameters in the H band for the calibrators from the JMMC angular diameter catalog (Bourgés et al. 2014): (1) HD 6319, θUDH = 0.740 ± 0.078 mas; (2) HD 12918, θUDH = 0.622 ± 0.058 mas; (3) HD 42855, θUDH = 0.758 ± 0.078 mas; and (4) HD 204149 θUDH = 0.671 ± 0.065 mas.
a Indicates nights where we detected the Ab companion.Download table as: ASCIITypeset image
Each observation consisted of recording 10 minutes of fringe data on Polaris followed by a shutter sequence to measure backgrounds, foregrounds, and the ratio of light between the fringe data and the photometric channels for each telescope. We monitored the interferometric transfer function by observing unresolved calibrator stars before and after each observation of Polaris. The calibrators were selected using the SearchCal software 15 (Bonneau et al. 2011) provided by the Jean-Marie Mariotti Center (JMMC). The calibrators and their adopted angular diameters (Bourgés et al. 2014) are listed in Table 1.
The data were reduced using the standard pipelines for MIRC (Monnier et al. 2007) and MIRC-X 16 (version 1.3.5; Anugu et al. 2020). The pipelines produce squared visibilities and triple products for each baseline and spectral channel. We used an integration time of 30 s for improved detection of the faint companion located at separations that ranged from 30 to 85 mas. We also produced OIFITS files (see Section 3.2) that were averaged over each 10 minute observing block for measuring the angular diameter and imaging the surface of Polaris Aa. We used a calibration script written in IDL by J. D. Monnier with the "deep cleaning" option to remove outliers. The reduced and calibrated OIFITS files will be available through the JMMC Optical Interferometry Database 17 (OIDB) An example of data collected on UT 2019 September 2 is displayed in Figure 1.
Figure 1. (u, v) coverage (left), squared visibilities (middle), and closure phase data (right) for the CHARA MIRC-X observations of Polaris on UT 2019 September 2. The closure phase data are plotted against the spatial frequency of the longest baseline in the closed triangle.
Download figure:
Standard image High-resolution imageThere were occasional offsets and more scatter than expected in some of the uncalibrated visibilities, particularly on the baselines including the E2 telescope in 2021 April. These discrepancies showed up between different calibrators and sometimes within a data set on the same target. Figure 2 shows an example where the visibilities on the E1–E2 baseline scatter upward during the observation of calibrator HD 204149 and during the second set on Polaris. In both of these cases, the discrepant visibilities appeared after a brief pause in the data collection to realign the starlight into the MIRC-X fibers. We could not find a definitive cause for the discrepant observations; it could be related to vibrations in the E2 delay line cart while tracking at very slow speeds in the north or telescope oscillations while pointing at the pole. We inspected the visibility transfer functions from each night to reject measurements that were clearly discrepant.
Figure 2. Visibility transfer function for the E1–E2 baseline on UT 2021 April 2 for the E1E2W1W2 configuration. The calibrators are marked by the orange shaded regions. The visibilities of Polaris have been multiplied by a factor of 4 to make them more visible on the plot. Circled in blue are two regions showing discrepant visibilities on Polaris and calibrator HD 204149.
Download figure:
Standard image High-resolution imageThe angular diameters and binary separations computed in Section 3 were multiplied by factors of 1.004 ± 0.0025 for MIRC and divided by 1.0054 ± 0.0006 for MIRC-X (J. D. Monnier 2022, private communication). This is equivalent to adjusting the respective wavelengths reported in the OIFITS files by the same factors.
3. Data Analysis
3.1. Diameter Measurements of Polaris Aa
We began our analysis of the interferometric data by fitting the squared visibility amplitudes for the angular diameter of Polaris Aa. The limb darkening was parameterized with the linear function Iλ
(μ) = Iλ
(1)[1 − uλ
(1 − μ)] (Hanbury Brown et al. 1974), with  , where ζ is the angle between the line of sight and a surface element of the star. We solved for the limb-darkened diameter (θLD), limb-darkening coefficient (uλ
), and visibility scaling factor (V0) to account for visibility miscalibrations or the presence of extended flux. The squared visibilities of the limb-darkened model are multiplied by V0 before comparing with the measured values. We first performed a grid search through the three parameters to find the best fit and then followed a Monte Carlo bootstrap approach with 1000 iterations to determine uncertainties. For each bootstrap iteration, we randomly selected measurements with repetition to construct a new set of visibilities with some measurements repeated and some left out. We then applied Gaussian uncertainties to the resampled measurements and fit a limb-darkened model using the IDL MPFIT package (Markwardt 2009) to optimize the fit for each iteration. We adopted the standard deviation of the bootstrap distributions as the uncertainties on each parameter. The angular diameters had been corrected using the wavelength calibration factors discussed in Section 2. To minimize scatter in the observations, the angular diameters were fit to the squared visibilities averaged over the 10 minute observing sets. The results from the diameter fits are presented in Table 2.
, where ζ is the angle between the line of sight and a surface element of the star. We solved for the limb-darkened diameter (θLD), limb-darkening coefficient (uλ
), and visibility scaling factor (V0) to account for visibility miscalibrations or the presence of extended flux. The squared visibilities of the limb-darkened model are multiplied by V0 before comparing with the measured values. We first performed a grid search through the three parameters to find the best fit and then followed a Monte Carlo bootstrap approach with 1000 iterations to determine uncertainties. For each bootstrap iteration, we randomly selected measurements with repetition to construct a new set of visibilities with some measurements repeated and some left out. We then applied Gaussian uncertainties to the resampled measurements and fit a limb-darkened model using the IDL MPFIT package (Markwardt 2009) to optimize the fit for each iteration. We adopted the standard deviation of the bootstrap distributions as the uncertainties on each parameter. The angular diameters had been corrected using the wavelength calibration factors discussed in Section 2. To minimize scatter in the observations, the angular diameters were fit to the squared visibilities averaged over the 10 minute observing sets. The results from the diameter fits are presented in Table 2.
Table 2. Limb-darkened Diameter Fits for Polaris Aa
| UT Date | HJD | Tmax | θLD | uλ | V0 | θfxu | Nvis |
|---|---|---|---|---|---|---|---|
| (mas) | (mas) | ||||||
| 2016 Sep 12 | 57643.736 | 57641.7504 | 3.1257 ± 0.0169 | 0.083 ± 0.044 | 1.2089 ± 0.0298 | 3.1370 ± 0.0169 | 96 |
| 2016 Nov 18 | 57710.744 | 57709.2759 | 3.1042 ± 0.0277 | 0.156 ± 0.064 | 0.8628 ± 0.0501 | 3.0937 ± 0.0277 | 96 |
| 2018 Aug 27 | 58357.744 | 58356.7171 | 3.1769 ± 0.0133 | 0.127 ± 0.037 | 1.2848 ± 0.0350 | 3.1749 ± 0.0133 | 360 |
| 2018 Aug 27 | 58357.946 | 58356.7171 | 3.1811 ± 0.0083 | 0.125 ± 0.033 | 1.2695 ± 0.0296 | 3.1801 ± 0.0083 | 360 |
| 2019 Apr 9 | 58582.815 | 58579.1471 | 3.1278 ± 0.0087 | 0.119 ± 0.024 | 1.2352 ± 0.0145 | 3.1283 ± 0.0087 | 216 |
| 2019 Apr 9 | 58582.970 | 58579.1471 | 3.1386 ± 0.0076 | 0.136 ± 0.023 | 1.3896 ± 0.0184 | 3.1351 ± 0.0076 | 180 |
| 2019 Sep 2 | 58728.777 | 58726.1087 | 3.1095 ± 0.0129 | 0.074 ± 0.038 | 1.0904 ± 0.0182 | 3.1223 ± 0.0129 | 78 |
| 2019 Sep 2 | 58728.868 | 58726.1087 | 3.1392 ± 0.0065 | 0.186 ± 0.018 | 1.1135 ± 0.0079 | 3.1194 ± 0.0065 | 372 |
| 2021 Apr 2 | 59306.839 | 59306.0020 | 3.1377 ± 0.0061 | 0.089 ± 0.018 | 0.9053 ± 0.0066 | 3.1468 ± 0.0061 | 576 |
| 2021 Apr 2 | 59306.927 | 59306.0020 | 3.1484 ± 0.0078 | 0.065 ± 0.025 | 1.0072 ± 0.0108 | 3.1588 ± 0.0078 | 192 |
| 2021 Apr 2 | 59306.974 | 59306.0020 | 3.1848 ± 0.0066 | 0.167 ± 0.018 | 0.8198 ± 0.0064 | 3.1750 ± 0.0066 | 384 |
| 2021 Apr 3 | 59307.982 | 59306.0020 | 3.1747 ± 0.0054 | 0.189 ± 0.014 | 1.1104 ± 0.0090 | 3.1542 ± 0.0054 | 660 |
| 2021 Apr 4 | 59308.727 | 59306.0020 | 3.1179 ± 0.0055 | 0.089 ± 0.015 | 1.1564 ± 0.0111 | 3.1267 ± 0.0055 | 594 |
| 2021 Apr 4 | 59308.845 | 59306.0020 | 3.1289 ± 0.0048 | 0.069 ± 0.016 | 1.0364 ± 0.0088 | 3.1388 ± 0.0048 | 792 |
Download table as: ASCIITypeset image
We measured a mean diameter of θLD = 3.143 ± 0.027 mas and a mean limb-darkening coefficient of uλ = 0.120 ± 0.043. At the Gaia distance of 136.90 ± 0.34 pc this corresponds to a mean radius of 46.27 ± 0.42 R⊙. On most nights, the scaling factor V0 was greater than 1.0, indicating that the V2 measurements are higher than the limb-darkened model. This implies a "negative" background flux, indicating that the scaling term likely arises because of a miscalibration of the visibilities, rather than a physical cause like extended flux outside the field of view. The calibration issues discussed in Section 2, as well as uncertainties in the partially resolved calibrator diameters, could have contributed to the miscalibration. The mean diameter is consistent within the uncertainties with the interferometric diameter measured with the FLUOR instrument at the CHARA Array (Mérand et al. 2006). However, the calibration of the MIRC/MIRC-X visibilities was not accurate enough to confirm the presence of the extended circumstellar envelope reported by Mérand et al. (2006).
To investigate whether we see changes in the diameter over the 4 day pulsation cycle, we fit the diameters separately for each configuration observed on each night as shown in Table 2. We adopted the ephemeris of Berdnikov & Pastukhova (1995) for the times of maximum light:

To account for the changing pulsation period, we used the O–C diagram in Figure 6 of Torres (2023) to calculate the times of maximum light nearest to each angular diameter measurement. The columns in Table 2 are the date of the observation, the Heliocentric Julian Date (HJD) –2,400,000, the time of maximum light used to compute the phase, the angular diameter and the limb-darkening coefficient, the scaling factor, the angular diameter from a fixed limb-darkening coefficient uλ = 0.120, and the number of visibility measurements. We plot the limb-darkened diameters with the fixed limb-darkening coefficient against the pulsation phase in Figure 3. The dashed line represents the mean angular diameter, and the dotted lines show 0.4% variation in diameter expected from pulsation (Moskalik & Gorynya 2005). The standard deviation of the mean diameter is 2.1 times larger than the variation expected from pulsation. Cepheids are expected to reach a minimum angular diameter around phase 0.8, which is roughly consistent with our measurements. However, the variations in the measured diameters could also be impacted by the visibility miscalibrations discussed in Section 2.
Figure 3. Limb-darkened diameters of Polaris Aa plotted against the pulsation phase. The dashed line represents the mean angular diameter, and the dotted lines show 0.4% variation in diameter expected from pulsation (Moskalik & Gorynya 2005).
Download figure:
Standard image High-resolution image3.2. Surface Imaging of Polaris Aa
The limb-darkened diameter model does a reasonable job fitting the squared visibility amplitudes. However, the strong nonzero and non-180° closure phases (see Figure 1) suggest the presence of asymmetries on the surface of Polaris Aa. Initial modeling of the data indicated that these strong deviations in the closure phases are not produced by the faint binary companion Ab. Modeling with PMOIRED 18 (Mérand 2022) and a custom-made routine in IDL, indicates that a few starspots on the surface of Polaris Aa can account for most of the closure phase signal. However, the size, location, and contrast of the spots are not well constrained due to the limited (u, v) coverage during the observations.
We also reconstructed images of the stellar surface of Polaris Aa using SQUEEZE 19 (Baron et al. 2010, 2012), SURFING (e.g., Roettenbacher et al. 2016), and ROTIR 20 (Baron 2020). Both SURFING and ROTIR perform the image reconstructions on the surface of a spheroid, constraining the size and shape of the star, which is important given the limited (u, v) coverage of the observations. ROTIR is written in Julia and uses the OITOOLS libraries, 21 a package for visualizing, modeling, and imaging interferometric data. We used the total variation regularizer with a weight of 0.01–0.05 for ROTIR. To prepare the OIFITS files for imaging, we corrected the visibilities for each individual data set using V0 scaling factors computed from limb-darkened diameter fits; we used the data averaged over the 10 minute observing sets. We merged together the data sets from all configurations on a given night to improve the (u, v) coverage for the image reconstructions. For the data from 2021 April, we merged the data together from the three consecutive nights.
Figure 4 shows the image of Polaris Aa reconstructed with SURFING and ROTIR for the epoch with the most complete (u, v) coverage from UT 2021 April 2, 3, and 4. Both images show a large bright spot to the north of center. We show the SURFING and ROTIR images from four different nights and the corresponding (u, v) coverage in Figure 5. All of the images show spots on the surface; however, some of the surface features could be created by artifacts in the reconstruction process due to gaps in the (u, v) coverage or systematic errors in the visibility calibration. The bottom row in Figure 5 shows reconstructed images from simulated data of a simple limb-darkened model without spots and with the same (u, v) sampling of Polaris to show which features are likely to be artifacts and which are likely to be spots on the surface. The contrast of the surface spots in the real data is larger than the contrast in the simulated limb-darkened disk data. In addition to having much lower contrast, the spots in the simulated data are distributed in point-symmetric patterns around the center of the star. The spots in the real data that do not follow these point-symmetric patterns are more likely to be true features on the stellar surface. Changing the simulated noise in the limb-darkened models slightly changes the shape and orientation of the artifacts in the simulated images; however, the large-scale structure of the patterns remains consistent between iterations with different simulated noise. The mirroring of bright and dark spots about the origin during some of the Polaris epochs is likely an artifact of the reconstruction process; however, these features are indicative of an asymmetry in brightness distribution. The interferometric data and observables extracted from the reconstructed images are shown in Appendix A.
Figure 4. Surface images of Polaris Aa reconstructed using SURFING (left) and ROTIR (right) on the merged data set from UT 2021 April 2, 2021 April 3, and 2021 April 4.
Download figure:
Standard image High-resolution imageFigure 5. Surface images of Polaris Aa reconstructed from the CHARA data on four different nights. The top row shows the (u, v) coverage, the second row shows the Polaris images reconstructed using SURFING, the third row shows images reconstructed using ROTIR, and the bottom row shows images reconstructed from simulated data of a limb-darkened disk model without spots and with the same (u, v) sampling as the Polaris data. The simulated data highlight artifacts in the reconstruction from gaps in the (u, v) coverage. For the ROTIR images, the standard deviation in the surface temperature is listed in the upper right corner of each panel.
Download figure:
Standard image High-resolution image3.3. Binary Positions of Polaris Aa, Ab
We used the data sets with 30 s integration times to search for the faint companion (Polaris Ab). The shorter integration time reduces time smearing of the companion signal given the separations of 40–85 mas expected from the previous orbit fit. To account for the asymmetries on the surface of Polaris Aa, we first reconstructed images with SQUEEZE using all of the data from a given night. We then used a modified version of the IDL Binary Grid Search Procedure 22 (Schaefer et al. 2016) where we extract visibilities and closure phases directly from the reconstructed image of Polaris Aa and analytically add in the companion. We started the grid search at the expected location of the binary based on the orbit computed by Evans et al. (2018) and searched within ΔR.A. = ± 20 mas and Δdecl. = ±20 mas from the initial values. We applied a correction for bandwidth smearing to the binary fit. The results from the binary grid search are shown in Appendix B.
We detected the Ab companion on five nights; these nights are indicated by a superscript next to the UT date in Table 1. On the nights with nondetections, the data quality was poor (e.g., 2016 November 18) or Polaris Ab was located outside of the interferometric field of view given by λ2/Δλ. The field of view corresponds to 50 mas in the low spectral resolution mode of MIRC and MIRC-X, so with an expected separation of ∼70 mas, we suspect that bandwidth smearing compromised the binary signal on UT 2018 August 27 and 2019 April 9. We were able to recover the detection of the companion on subsequent dates when we used the higher spectral resolution Prism102 and Grism190 modes with a field of view of 100 and 190 mas, respectively.
The average contrast of the companion was ΔH = 7.8 ± 0.4 mag, beyond the typical detection limits of the MIRC and MIRC-X instruments (Gallenne et al. 2015). To improve our confidence in the solutions, we also performed the binary grid search separately for each configuration observed on a given night. For the nights with high confidence solutions, the separations measured from each configuration separately were consistent with the results based on the full night of data. Additionally, the three successive nights in 2021 April produced consistent binary solutions.
We used a bootstrap approach with 100 iterations to estimate the uncertainties based on the 67.5% confidence ellipses for two parameters from the bootstrap distributions. These errors are added in quadrature with the uncertainties from the wavelength calibration. The best-fit binary positions (corrected for wavelength calibration) and flux ratios (fAb/fAa) are listed in Table 3. The positions of Polaris Ab relative to Aa are given as the separation (ρ) and position angle (PA) measured east of north. We also list the separations projected into R.A. (Δα) and decl. (Δδ). The error ellipses are given by the semimajor axis (σmaj), semiminor axis ( ), and the PA of the major axis (σPA). The dates are given as HJD and Julian year (JY). In Table 3, we also collected the HST astrometric measurements reported by Evans et al. (2008, 2018) in both polar and Cartesian coordinates. These papers reported the dates in Besselian years, which we have converted to JY.
), and the PA of the major axis (σPA). The dates are given as HJD and Julian year (JY). In Table 3, we also collected the HST astrometric measurements reported by Evans et al. (2008, 2018) in both polar and Cartesian coordinates. These papers reported the dates in Besselian years, which we have converted to JY.
Table 3. Relative Astrometric Position of the Polaris Ab Companion
| HJD | JY | ρ | PA | Δα | Δδ | σmaj |

| σPA | fAb/fAa |
|---|---|---|---|---|---|---|---|---|---|
| −2,400,000 | (mas) | (deg) | (mas) | (mas) | (mas) | (mas) | (deg) | ||
| CHARA | |||||||||
| 57643.735 | 2016.6974 | 33.008 | 71.696 | 31.338 | 10.366 | 5.757 | 1.159 | 18.49 | 0.00089 ± 0.05838 |
| 58728.831 | 2019.6683 | 75.537 | 340.239 | −25.538 | 71.088 | 0.833 | 0.547 | 40.73 | 0.00072 ± 0.00744 |
| 59306.890 | 2021.2509 | 84.507 | 315.900 | −58.810 | 60.686 | 1.200 | 0.663 | 94.49 | 0.00110 ± 0.00789 |
| 59307.982 | 2021.2539 | 84.447 | 315.787 | −58.888 | 60.527 | 10.736 | 3.954 | 123.45 | 0.00070 ± 0.02214 |
| 59308.785 | 2021.2561 | 84.232 | 315.669 | −58.861 | 60.252 | 0.880 | 0.804 | 135.12 | 0.00045 ± 0.00363 |
| Speckle | |||||||||
| 60237.913 | 2023.800 | 98.8 | 286.7 | −94.6 | 28.4 | 5.3 | 4.2 | 0.0 | ... |
| HST | |||||||||
| 53585.488 | 2005.5866 | 172.4 | 231.407 | −134.75 | −107.54 | 2.1 | 2.1 | 0.0 | ... |
| 53961.416 | 2006.6158 | 169.6 | 226.385 | −122.79 | −116.99 | 3.1 | 3.1 | 0.0 | ... |
| 54298.514 | 2007.5387 | 180.0 | 223.000 | −122.76 | −131.64 | 20.0 | 20.0 | 0.0 | ... |
| 55153.597 | 2009.8798 | 150.0 | 216.000 | −88.17 | −121.35 | 20.0 | 20.0 | 0.0 | ... |
| 56835.302 | 2014.4841 | 85.0 | 175.000 | 7.41 | −84.68 | 20.0 | 20.0 | 0.0 | ... |
Note. Positions in Table 3 are for J2000.
Download table as: ASCIITypeset image
3.3.1. Confirmation of Binary Positions with CANDID
We confirmed the companion detections using the Companion Analysis and Non-detection in Interferometric Data (CANDID) tool
23
(Gallenne et al. 2015). CANDID is a set of Python tools allowing us to search systematically for companions and estimate detection limits using all interferometric observables. We used the implemented bootstrap function to estimate the uncertainties on our previous parameters. In CANDID, limb darkening is parameterized with a power-law function Iλ
(μ) = Iλ
(1)μ , and we chose to fix this parameter to 0.15. Bootstrapping is performed on the MJDs with our previous fitted parameters and using 1000 bootstrap samples. From the distribution, we took the median value and the maximum value between the 16th and 84th percentiles as uncertainty for the flux ratio and angular diameter. For the fitted astrometric position, the error ellipse is derived from the bootstrap sample (using a principal component analysis). The positions and uncertainties measured with CANDID were consistent with those determined from the IDL grid search procedure.
, and we chose to fix this parameter to 0.15. Bootstrapping is performed on the MJDs with our previous fitted parameters and using 1000 bootstrap samples. From the distribution, we took the median value and the maximum value between the 16th and 84th percentiles as uncertainty for the flux ratio and angular diameter. For the fitted astrometric position, the error ellipse is derived from the bootstrap sample (using a principal component analysis). The positions and uncertainties measured with CANDID were consistent with those determined from the IDL grid search procedure.
4. Speckle Observations of Polaris
Polaris was observed using the technique of speckle interferometry at the Astrophysical Research Consortium (ARC) 3.5 m telescope at APO on 2023 October 19 and 20. The speckle camera used was the Differential Speckle Survey Instrument (DSSI; Horch et al. 2009), which is currently a visitor instrument at APO. DSSI takes speckle patterns in two filters simultaneously; for the Polaris observations, we used filters with center wavelengths of 692 nm and 880 nm and FWHMs of 40 nm and 50 nm, respectively. On each night, a total of 9000 short-exposure images were recorded in each filter and stored in nine FITS files, each of which consisted of a 1000-frame stack of 256 × 256 pixel frames. The exposure time of individual frames was 40 ms, and the seeing was approximately 0 9 on both nights.
9 on both nights.
The reduction and calibration of DSSI speckle data at APO is described in Davidson et al. (2024); briefly, we bias subtract and form the spatial frequency power spectrum of individual frames, coadding these in the Fourier domain to arrive at a summed power spectrum for each data file. We then deconvolve by dividing by the power spectrum of a bright point source observed in the same way. The result for a binary star is a pure fringe pattern, which we then fit using a downhill simplex algorithm as described in Horch et al. (1997). The fringe spacing, orientation, and depth of the fringe minima determine the separation, position angle, and magnitude difference of the pair. In this analysis, we do not determine the quadrant of the secondary star; there is a 180° ambiguity in the position angle due to the fact that the power spectrum has no phase information. For the 2023 October speckle run at APO, the pixel scale and orientation were obtained using a combination of several binaries with extremely well-determined orbits and slit-mask observations, as described in Davidson et al. (2024). These methods resulted in a pixel scale with an uncertainty of approximately 0.24% and offset angles between pixel axes and celestial coordinates that are uncertain at the 0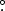 1 level.
1 level.
Polaris presents a complication in the speckle analysis because it is a system with a large magnitude difference that is observed at an airmass of near 2.0 from Apache Point. The airmass adds dispersion to the speckle patterns, stretching speckles out on the image plane in a direction leading toward the zenith. This then changes the shape of the power spectrum and could affect the fringe fitting results. To have a good estimate of the speckle transfer function for a particular DSSI observation, a bright unresolved star is typically observed near in time and close in sky position to the star of interest. In the case of Polaris, since it was not possible to have as close a match in sky position as we typically use, we instead observed a bright unresolved star at low airmass, and then applied a dispersion model to that observation so that it matched Polaris's zenith angle and azimuth exactly. This removed most of the effect of the dispersion, but a further correction was applied by allowing for additional free parameters in the fringe fit to account for any residual dispersion in the Fourier domain. In this way, it was possible to determine relatively consistent relative astrometry and photometry of the system for the subsample of the files analyzed that had the lowest reduced chi-squared values from the fringe fitting procedure.
The measurements from the best sequences in the two nights of data resulted in the following average relative position: Δα = − 0 0902 ± 0
0902 ± 0 0053 and Δδ = + 0
0053 and Δδ = + 0 0404 ± 0
0404 ± 0 0042, for the equinox of the date of observation (JY 2023.7999). These correspond to polar coordinates θ = 294
0042, for the equinox of the date of observation (JY 2023.7999). These correspond to polar coordinates θ = 294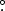 1 ± 3
1 ± 3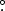 7 and ρ = 0
7 and ρ = 0 0988 ± 0
0988 ± 0 0052. Because of the dispersion complication noted above, we were not able to derive a reliable measure of the magnitude difference between Polaris and its companion.
0052. Because of the dispersion complication noted above, we were not able to derive a reliable measure of the magnitude difference between Polaris and its companion.
Given that the rest of the astrometric measurements in this work are effectively referred to the equinox J2000, we applied rigorous precession to our result above in order to reduce it to that same frame of reference. The position angle correction is −7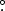 4. We obtained Δα = −0
4. We obtained Δα = −0 0946 ± 0
0946 ± 0 0053 and Δδ = +0
0053 and Δδ = +0 0284 ± 0
0284 ± 0 0042 (J2000).
0042 (J2000).
5. Orbit Fitting
5.1. Radial Velocities
The orbital analysis depends on the combination of two data sets, the RVs and relative astrometry. The RV data set is very large and made up of measurements from many sources to cover multiple cycles of the 30 yr orbit of Polaris Aa–Ab. We used the complete set of 3659 RVs with pulsation removed that are tabulated in Table 3 of Torres (2023). 24 To those we added an additional 16 Hermes velocities from the program VELOCE I (Anderson et al. 2024). The data were prepared using the template approach detailed in Anderson (2019). Initially, we applied the RV jitter and offset terms in Table 5 of Torres (2023) and the additional Hermes data (jitter is as defined in Torres 2023; the uncertainty for each data set from the orbit fitting). After experimentation and preliminary fits, the offsets and jitter were redetermined as listed in Table 4. The sources and references are as listed in Table 5 of Torres (2023). Successive pairs of columns to the right provide the RV offset and jitter for the original orbit in Torres (2023) and the solution for RVs and CHARA and HST astrometry here.
Table 4. Corrections to Radial-velocity Sources
| Source | Torres (2023) | RV + Astrom | ||
|---|---|---|---|---|
| Offset | Jitter | Offset | Jitter | |
| (km s−1) | (km s−1) | (km s−1) | (km s−1) | |
| 1 Roemer (1965) | ⋯ | 0.681 | ⋯ | 0.680 |
| 2 Hartmann (1901) | +1.39 | 0.51 | +1.43 | 0.52 |
| 3 Kustner (1908) | +1.05 | 0.75 | +0.94 | 0.83 |
| 4 Arellano Ferro (1983) + Kamper (1996) | +1.027 | 0.524 | +1.001 | 0.580 |
| 5 Dinshaw et al. (1989) | −11.829 | 0.469 | −11.694 | 0.450 |
| 6 Gorynya et al. (1992) | +1.488 | 0.500 | +1.375 | 0.498 |
| 7 Hatzes & Cochran (2000) | −14.117 | 0.027 | −14.242 | 0.027 |
| 8 Usenko et al. (2020) | +0.068 | 0.387 | +0.100 | 0.409 |
| 9 Kamper & Fernie (1998) | −0.222 | 0.1061 | −0.323 | 0.1065 |
| 10 Eaton (2020) | +1.120 | 0.0444 | +1.156 | 0.0398 |
| 11 Lee et al. (2008) | −17.794 | 0.1103 | −17.772 | 0.1124 |
| 12 Buecke (2021) | −18.387 | 0.0976 | −18.387 | 0.150 |
| 13 Anderson (2019) | +0.551 | 0.0977 | +0.622 | 0.1125 |
| 14 Anderson et al. (2024) | ⋯ | ⋯ | +0.440 | 0.103 |
Download table as: ASCIITypeset image
5.2. Orbit
The astrometry data set has only 11 two-dimensional data points that cover only 16 yr, or half the orbit.
Table 5 lists the orbital parameters from the spectroscopic RV orbit computed by Torres (2023) and Anderson et al. (2024) and a fit to only the visual orbit computed through a Newton Raphson technique using the IDL orbit fitting library 25 described by Schaefer et al. (2016). The orbital parameters include the orbital period Porb, time of periastron passage Tp, eccentricity e, argument of periastron with reference to the primary ω, primary RV amplitude K1, systemic velocity γ, longitude of ascending node Ω for J2000, inclination i, and angular semimajor axis a. The eccentricity and ωAa differ by 1.4σ and 2.3σ, respectively, between the spectroscopic and visual orbits.
Table 5. Orbit Fitting Results
| Parameter | RV Only | Astrometry Only | σ Weights | N σ Weights | Replicated |
|---|---|---|---|---|---|
| Porb (yr) | 29.4330 ± 0.0079 | 29.49 ± 0.35 | 29.448 ± 0.012 | 29.384 ± 0.017 | 29.416 ± 0.028 |
| Tperi (JY) | 2016.801 ± 0.011 | 2016.781 ± 0.049 | 2016.857 ± 0.012 | 2016.833 ± 0.017 | 2016.831 ± 0.044 |
| e | 0.6195 ± 0.0015 | 0.6309 ± 0.0079 | 0.6290 ± 0.0016 | 0.6336 ± 0.0235 | 0.6354 ± 0.0066 |
| ωAa (°) | 303.04 ± 0.34 | 305.22 ± 0.95 | 304.33 ± 0.26 | 304.46 ± 3.17 | 304.54 ± 0.84 |
| K1 (km s−1) | 3.7409 ± 0.0075 | ... | 3.738 ± 0.010 | 3.796 ± 0.311 | 3.762 ± 0.025 |
| γ (km s−1) | −16.084 ± 0.025 | ... | −16.0970 ± 0.0047 | −16.110 ± 0.170 | −16.1024 ± 0.0084 |
| Ω (°) | ... | 202.16 ± 0.94 | 200.16 ± 0.70 | 201.20 ± 2.59 | 201.28 ± 1.18 |
| i (°) | ... | 127.82 ± 0.77 | 128.57 ± 1.00 | 127.707 ± 3.191 | 127.57 ± 1.21 |
| a (mas) | ... | 129.07 ± 1.18 | 127.72 ± 1.85 | 129.371 ± 5.432 | 129.55 ± 2.05 |
| Reference | (Torres 2023) | Section 5.2 | Section 5.3 | Section 5.4 | Section 5.5 |
| Mtot (M⊙) | 6.35 ± 0.23 | 6.16 ± 0.28 | 6.4153 ± 0.7576 | 6.45 ± 0.31 | |
| MAa (M⊙) | ... | ... | 4.87 ± 0.26 | 5.0864 ± 0.6245 | 5.13 ± 0.28 |
| MAb (M⊙) | ... | ... | 1.295 ± 0.019 | 1.3289 ± 0.2702 | 1.316 ± 0.028 |
Note. Masses computed assuming a Gaia distance of 136.90 ± 0.34 pc.
Download table as: ASCIITypeset image
Our methods for fitting the RVs and astrometry simultaneously are described in the following subsections. It was realized early on that the analysis approach is particularly important since the orbit has a substantial eccentricity. In a preliminary solution weighted solely by the errors on the data points in the two data sets, the HST astrometry was systematically offset from the orbit. The eccentricity and ωAa are set essentially by the large number of RVs. We explored several approaches to combine the different data sets. The various weighting methods are described in more detail below with the orbital parameters from each solution listed in Table 5.
5.3. Weights Based on Measurement Errors
To determine the orbital parameters, we simultaneously fitted the RVs and astrometric position using a Markov Chain Monte Carlo (MCMC) routine, 26 whose log-likelihood function is given as (Gallenne et al. 2019a)

In our previous works on binary Cepheid systems with astrometric data (see, e.g., Gallenne et al. 2019b, 2018), both the pulsation and orbital motions of the Cepheids were fitted together with the astrometry. In this work, we decided to ignore the pulsation motion of the Cepheid by directly fitting the pulsation-corrected RVs from Torres (2023). In this case, our RV model is simply defined as

in which V1 and σ1 denote the measured RV and uncertainties for Polaris, and V1m is the Keplerian velocity model characterized by Heintz (1978):

where γ is the systemic velocity, e is the eccentricity, ω is the argument of periastron, ν is the true anomaly, E is the eccentric anomaly, t is the observing date, Porb is the orbital period, Tp is the time of periastron passage, and K1 is the primary RV amplitude. The  measure for astrometry depends on the astrometric measurements as
measure for astrometry depends on the astrometric measurements as

in which  denote the relative astrometric measurements with the corresponding error ellipses, and (Δαm, Δδm) represent the astrometric model defined as
denote the relative astrometric measurements with the corresponding error ellipses, and (Δαm, Δδm) represent the astrometric model defined as

where Ω is the longitude of ascending node, i is the orbital inclination, and a is the angular semimajor axis.
As a starting point for our 100 MCMC walkers, we performed a least-squares fit using orbital values from Torres (2023) as first guesses. We then ran 100 initialization steps to well explore the parameter space and get settled into a stationary distribution. For all cases, the chain converged before 50 steps. Finally, we used the last position of the walkers to generate our full production run of 1000 steps, discarding the initial 50 steps. All the orbital elements are estimated from the distribution taking the median value and the maximum value between the 16th and 84th percentiles as uncertainty (although the distributions were roughly symmetrical).
Polaris is a single-lined spectroscopic binary that does not allow the individual masses to be determined independently without additional information. To this end, we adopt the Gaia distance for Polaris B (above). In our MCMC procedure, we included the parallax measurement using a normal distribution centered on 7.3045 mas with a standard deviation of 0.0178 mas. Masses are then derived with the following equations:

with MT = M1 + M2 the total mass in M⊙, a and ϖ in mas, Porb in yr, and K1 in km s−1.
Initially, when fitting the orbit simultaneously to the RVs and astrometry, we weighted each measurement by their respective uncertainties. We performed a similar fit weighted by measurement uncertainties using the IDL orbit fitting library, but with uncertainties computed through a bootstrap technique. The orbital parameters from this fit are listed in the "σ Weights" column of Table 5.
5.4. Weights Based on N σ
To more evenly weight the two data sets, we can compute an average χ2 statistic multiplying the χ2 from each data set by 1/N, where N is the number of data points (Mérand et al. 2015, Equation (5)). The total χ2 for the simultaneous fit then becomes

where NRV is the number of RV measurements and Nast is the number of astrometry data points. The orbital parameters are listed in the "N σ Weight" column of Table 5. Uncertainties in the orbital parameters were determined from MCMC distributions.
5.5. Replicating the Astrometric Measurements
Another weighting scheme is motivated by the Synthetic Minority Over-sampling Technique (SMOTE) used in the machine learning community (Chawla et al. 2002). In order to weight the two sets of measurements more evenly, we replicated each position measurement 167 times to give a roughly even number of observables (N = 167 × 11 × 2 = 3674). We applied random Gaussian uncertainties to the replicated measurements, creating a swarm of simulated observables for each data point. We then fit a simultaneous orbit to the RVs and the replicated positions using the IDL orbit fitting library. 27 We followed a Monte Carlo bootstrap approach to compute uncertainties. For each bootstrap iteration, we randomly selected from the 11 astrometric measurements, with repetition. We then applied Gaussian uncertainties to the resampled measurements and replicated each data point as described above. We repeated this process 1000 times and computed uncertainties in the orbital parameters from the standard deviation of the bootstrap distributions. The orbital parameters from this fit are listed in the "Replicated" column of Table 5. The spectroscopic and astrometric orbits are shown in Figure 6. The orbital parameters and uncertainties are consistent with the 1/N weighting method. The averaged χ2 in Section 5.4 underweights the RVs, while the replicated points overweight the astrometry; but both methods provide similar results in the end.
Figure 6. Spectroscopic (left) and astrometric (right) orbital fit of Polaris. The symbols for the measurements by HST ACS, HST WFPC2 and WFC3, CHARA, and APS speckle are shown in the figure. In addition to the best-fit orbit, overplotted in gray is a sample of 1000 orbits selected at random while estimating the bootstrapped uncertainties.
Download figure:
Standard image High-resolution imageIn summary, all three weighting schemes produced similar masses within the errors. As stated in Section 5.2, in the solution based on measurement errors (Section 5.3) of the astrometric points from HST ACS/HRC are systematically displaced from the orbit solution. Thus, the astrometry is poorly represented. This is possibly due to systematic errors in the historical RVs, which are difficult to quantify, and which may on their own be distorting the shape of the orbit and imposing that shape on the much less numerous astrometric measurements. For this reason, a solution giving higher weight to the astrometry (Section 5.5) is preferred with a mass of the Cepheid of 5.13 ± 0.28 (5%) M⊙.
6. Discussion
6.1. The Cepheid Mass
Approximately three-quarters of the 30 yr orbit of Polaris has now been observed with HST, CHARA, and speckle measurements. The resulting mass of the Cepheid is 5.13 ± 0.28 (5%) M⊙, which is larger than before the CHARA and speckle observations were included, but with smaller errors. The previous mass was 3.45 ± 0.75 M⊙ (Evans et al. 2018; based on a slightly different distance).
6.2. Cepheid Mass–Luminosity Relation
Cepheids provide a quantitative test of evolutionary calculations. In the case of Polaris, the mass derived here is combined with a luminosity to compare with theoretical predictions. For MW Cepheids in general, definitive luminosities will be produced by Gaia in the release that includes orbital fits in the analysis. For Polaris, we use the distance to Polaris B as discussed in Section 1.1. Since Polaris B is not a close binary, an orbit is not required in the Gaia solution.
Figure 7 shows the Cepheid mass–luminosity relation with the location of Polaris in comparison with the predictions from evolutionary calculations of several groups, which predict the luminosity for a given mass.
Figure 7. Cepheid mass–luminosity relation. The Milky Way Cepheids, Polaris (this work) and V1334 Cyg (Gallenne et al. 2018), are plotted as squares. LMC Cepheids (Pilecki et al. 2021) are plotted as asterisks. Overplotted are predictions from evolutionary tracks (Anderson et al. 2014; Anderson et al. 2016; Bono et al. 2016) for (1) long dashed line: MW metallicity, no main-sequence convective overshoot; (2) solid line: MW metallicity, moderate convective overshoot; (3) dotted line: MW metallicity, small convective overshoot and rotation; (4) short dashed line: LMC metallicity, moderate convective overshoot. Mass and luminosity are in solar units.
Download figure:
Standard image High-resolution imageFigure 7 includes V1334 Cyg, which has the most accurate Cepheid mass at present (Gallenne et al. 2018). The solution also provides an accurate (3%) distance to the system. It is a good comparison for Polaris since it has similar characteristics. It pulsates in the first overtone and has a period (luminosity) similar to Polaris. Also shown in Figure 7 are masses for LMC Cepheids in eclipsing binaries from Pilecki et al. (2021). Luminosities for the MW Cepheids are from the distance to Polaris (above) and V1334 Cyg. Luminosities for the LMC Cepheids are from Pilecki et al. (2021). The observed mass–luminosity combinations are compared with evolutionary predictions from Bono et al. (2016) and Anderson et al. (2014). The Bono tracks cover MW and LMC metallicities. For the MW the relations are shown for no main-sequence convective core overshoot and moderate overshoot. The Anderson relation is for main-sequence rotation and moderate convective overshoot. The lower metallicity of the LMC stars results in a higher luminosity than for solar abundance stars, as indicated by the models.
The determination of the mass of Polaris in this study is part of a series of studies to measure that of Cepheids. Additional MW Cepheids are to be added to Figure 7. However, the first indication is that in the examples so far (Polaris, V1334 Cyg, and the LMC Cepheids) the luminosity is larger than predicted by current evolutionary calculations.
6.3. Evolutionary Tracks
To explore the details of the calculation results, we provide Figure 8 updated from Figure 7 in Evans et al. (2018). Temperatures are from (B−V)0, as discussed in Evans et al. (2018). Figure 8 illustrates the location of Polaris and also V1334 Cyg with respect to evolutionary calculations for 4, 5, and 7 M⊙ from Georgy et al. (2013). The tracks contrast evolution for stars with zero rotational velocity on the main sequence and those with 0.95 breakup velocity. Both Polaris and V1334 Cyg are more luminous than the 5 M⊙ track in the blue loop, even for large main-sequence rotation. For a comparison between codes, Figure 8 in Evans et al. (2018) shows the location of Polaris compared with three sets of tracks for a 5 M⊙ model: Geneva (Georgy et al. 2013), MIST (Choi et al. 2016), and PARSEC 28 (based on the Bressan et al. 2012 group). All three sets of tracks are shown for zero initial main-sequence rotation; for the Geneva and MIST calculations, a track is also shown for substantial rotation. In this figure, the MIST tracks (both with and without substantial main-sequence rotation) approximately coincide with the Georgy tracks with rotation.
Figure 8. Polaris and V1334 Cyg compared with evolutionary tracks. For Polaris (filled square) and V1334 Cyg (filled triangle) the mass in M⊙ is listed next to the star name. The evolutionary tracks from Georgy et al. (2013) are for 4, 5, and 7 M⊙ in colors of green, black, and red, respectively. Solid lines are for zero rotational velocity on the main sequence; dashed lines have 0.95 breakup velocity. Luminosity is in solar units; temperature is in Kelvin.
Download figure:
Standard image High-resolution imageOne further criterion for the comparison between observed masses and evolutionary tracks is that Cepheids are found in a region of the luminosity–temperature diagram (Figure 8) where the blue loops penetrate the instability strip. This was a motivation of the exploration of the effect of rotation in main-sequence progenitors (Anderson et al. 2014), since increasing the main-sequence core convective overshoot increases luminosity at the Cepheid phase, but truncates the blue loops. Evolutionary tracks for additional masses probe this further.
6.4. Properties of Polaris
This study provides astrometry from CHARA interferometry and APO speckle observations for the Polaris Aa and Ab system. When combined with previous HST observations and RVs (Torres 2023), a mass of 5.13 ± 0.28 M⊙ is derived. The observed luminosity for Polaris is brighter than predicted by current evolutionary tracks. The predicted luminosity depends on the rotation of the main-sequence progenitor, but Figure 8 shows that Polaris is at least 0.4 mag brighter than the predicted tracks including a small correction from the 5 M⊙ tracks to the mass of Polaris (based on a 0.5 critical breakup velocity; Anderson et al. 2014). This study is part of a series of studies of Cepheid masses using interferometry as well as Gaia astrometry to examine these questions.
In the case of Polaris several of its properties are unusual in the context of Cepheids. It pulsates in the first overtone, which may be linked with the rapid period change. Overtone pulsators have more instability in their pulsation periods, which can sometimes be interpreted as rapid period change. The variation in pulsation amplitude may also be related to its pulsation mode. The recent discussion of velocities (Torres 2023) postulates that the "glitch" in pulsation may occur at periastron passage. This would add a new factor to the interpretation of the observations. It has been suggested for other Cepheids with a "phase jump" that they are likely to be binary systems (Csornyei et al. 2022). In summary, while these properties are unusual for Cepheids, they exist in other stars. Thus, Polaris fits in the framework of pulsating supergiants, particularly if orbital motion is included. While these characteristics complicate the interpretation of observations, all are found in stars without abnormal evolution.
The identification of starspots is consistent with several properties of Polaris. It has a very low pulsation amplitude, which sets it apart from full amplitude Cepheids. This may mean that the atmosphere is like that of a nonvariable supergiant, which have often indicators of activity. It is not clear how full amplitude pulsation affects the atmosphere and magnetic field in pulsators, so Polaris is an interesting test case.
Polaris has a couple of other characteristics that would be consistent with magnetically related spots. Polarization has been found (Barron et al. 2022). However, the polarization measurements look more like those of the nonvariable supergiant α Per than other Cepheids (Grunhut et al. 2010), but this may just reflect the very low pulsation amplitude. Polaris has also been detected in X-rays (Evans et al. 2022).
Our identification of starspots opens the prospect of determining a rotation period. It also can explain why additional periodicities have been difficult to find, since the distribution of spots is variable. The long-period (≃120 days) variation found by Lee et al. (2008), for instance, might be a rotation period. Periods of 40 and 60 days found by Anderson (2019) may be related.
Another possible interpretation of surface features on Polaris is convective supergranules as discussed by Schwarzschild (1975).
A final characteristic of the orbit of Polaris is the high eccentricity. This is often found in systems that have undergone three-body interaction, which would be consistent with the Cepheid being a merger product from a former triple system, as suggested by Evans et al. (2018). However, high eccentricity is frequently found in long-period systems (Shetye et al. 2024), so it does not require special conditions.
7. Summary and Future Work
The CHARA and APO observations of the Polaris Aa and Ab system have added to previous astrometric observations to cover approximately three-quarters of the orbit. The mass of the Cepheid that results from these data and the spectroscopic orbit is 5.13 ± 0.28 (5%) M⊙. The Cepheid is overluminous for this mass according to current calculations. Starspots have been identified in the CHARA images, providing another tool to use to investigate the Cepheid.
Further observations with CHARA and APO will provide additional coverage of the orbit and add to the determination of the mass.
Acknowledgments
This work is based upon observations obtained with the Georgia State University Center for High Angular Resolution Astronomy Array at Mount Wilson Observatory. The CHARA Array is supported by the National Science Foundation under grant Nos. AST-1636624 and AST-2034336. Institutional support has been provided from the GSU College of Arts and Sciences and the GSU Office of the Vice President for Research and Economic Development. Time at the CHARA Array was granted through the NOIRLab community access program (NOIRLab PropID: 2018B-0039; PI: N. Evans). P.K. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (project UniverScale, grant agreement 951549). S.K. acknowledges funding for MIRC-X from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Starting grant No. 639889 and Consolidated grant No. 101003096). J.D.M. acknowledges funding for the development of MIRC-X (NASA-XRP NNX16AD43G, NSF-AST 1909165). A.G. acknowledges the support of the Agencia Nacional de Investigación Científica y Desarrollo (ANID) through the FONDECYT Regular grant 1241073. R.M.R. acknowledges funding from the Heising-Simons Foundation 51 Pegasi b Fellowship. Support was provided to N.R.E. by the Chandra X-ray Center NASA Contract NAS8-03060. This research has received support from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant Agreement No. 947660). R.I.A. is funded by the Swiss National Science Foundation through an Eccellenza Professorial Fellowship (award PCEFP2_194638). This research is based on observations made with the Mercator Telescope, operated on the island of La Palma by the Flemish Community, at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias (observations from Anderson et al.). Hermes is supported by the Fund for Scientific Research of Flanders (FWO), Belgium, the Research Council of K.U. Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland, and the Thüringer Landessternwarte, Tautenburg, Germany.
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research made use of services provided by the Jean-Marie Mariotti Center (Aspro, SearchCal, and OIDB). The SIMBAD database, and NASA's Astrophysics Data System Bibliographic Services were used in the preparation of this paper.
The software used in this project are available from Squeeze (Fabien 2024a) and ROTIR (Fabien 2024b).
Appendix A: Interferometric Data Plots: Imaging Results
Figure 9 shows the visibilities and closure phases measured with CHARA MIRC-X averaged over 10 minute observing sets. The data (black circles) and observables extracted from the reconstructed images (red circles) are plotted in the top panels of each figure. The bottom panels show the residuals between the data and the image.
Figure 9.
Visibilities and closure phases measured with CHARA MIRC-X and averaged over 10 minute observing sets for Polaris on UT 2018 August 27. The black symbols are the measured values, while the red symbols are extracted from the ROTIR reconstructed image. The bottom panels show the residuals between the data and the image. (The complete figure set (4 images) is available.)
Download figure:
Standard image High-resolution imageAppendix B: Interferometric Data Plots: Binary Fits
Figure 10 shows the results from the binary fits to the CHARA MIRC-X interferometry using the 30 s integration time. Each figure shows the (u, v) coverage, the χ2 map from the binary grid search, the visibilities, and the closure phases. The χ2 maps are centered at the predicted location based on the updated orbit fit. The nights with reliable detections show a clear minimum in the χ2 indicated by the colored circles. The nights with unreliable binary fits show more ambiguity in the χ2 maps.
Figure 10.
Binary fit for Polaris on UT 2016 September 12. Top row: (u, v) coverage (left) and χ2 map from the binary grid search (right). In the χ2 map, the red, orange, yellow, green, blue, purple, large black, and small black symbols correspond to solutions within Δχ2 = 1, 4, 9, 16, 25, 36, 49, and >50 from the minimum χ2. Bottom row: the filled black circles show the squared visibilities (left) and closure phases (right) measured with MIRC-X using the 30 s integration time. The red crosses show the best-fit binary model. (The complete figure set (8 images) is available.)
Download figure:
Standard image High-resolution image












